Significance
Keypoints
- Propose two objectives for multi-class data description that separates latent ID and OOD samples by hypersphere
- Derive theoretical relationship between the proposed method and the Gaussian discriminant analysis
- Demonstrate performance of the proposed method quantitatively and qualitatively
Review
Background
Softmax classifier is one of the most widely adopted objective for training a deep neural network that can work on multi-class classification tasks.
Although the training samples are trained to maximize the softmax probability for the target classes, an out-of-distribution (OOD) sample with no corresponding target class tend to collapse most of the softmax probability into similar small values.
This means that the OOD sample latent is dragged towards to the origin without appropriate direction, creating random overlap with the in-distribution (ID) hyperplane of the softmax decision boundary.
Studies that incorporate the Mahalanobis distance address this limitation to some extent, but still inherits difficulty in indentifying unseen OOD samples during training.
This work is inspired by the Support Vector Data Description, which exploits kernel function with spherical boundary for novelty detection.
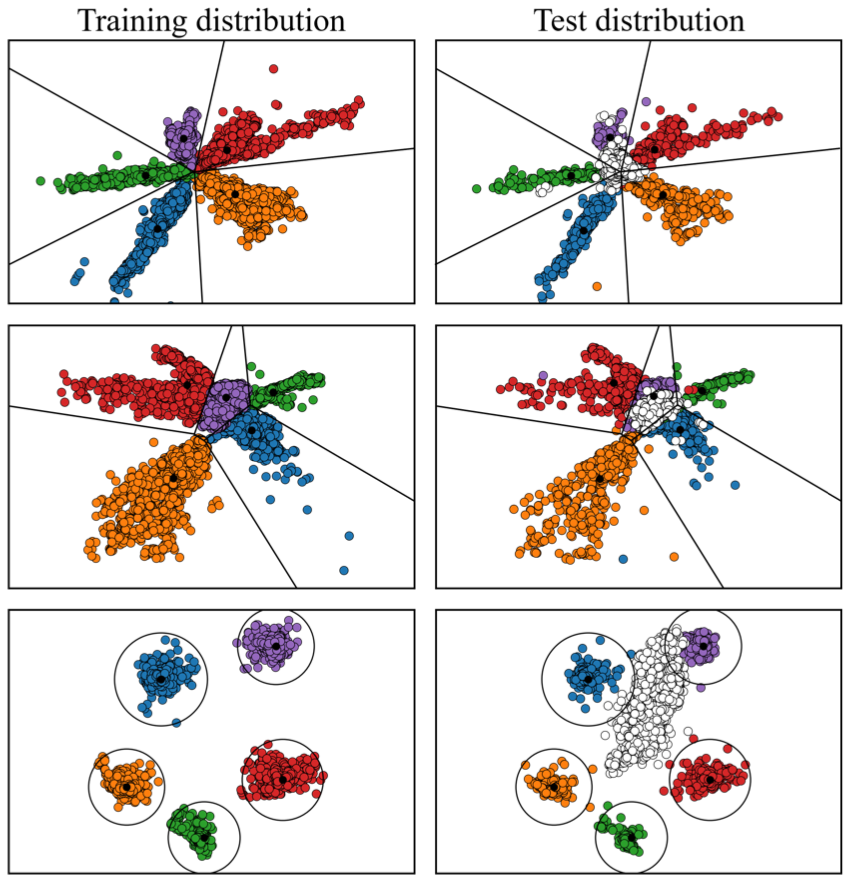Latent space of the Softmax / Mahalanobis / Proposed method (empty circles are unseen OOD samples)
Keypoints
Propose two objectives for multi-class data description that separates latent ID and OOD samples by hypersphere
Soft MCDD
The authors introduce an objective to model class boundaries as multiple hyperspheres, which includes learnable nonlinear function as a deep neural network $f(\cdot; \mathcal{W})$ where $\mathcal{W}$ is the set of network parameters. Given a set of training samples ${ (x_{1},y_{1}), … , (x_{N}, y_{N}) }$ from $K$ different classes, the objective is defined as \begin{equation}\label{eq:softmcdd} \underset{\mathcal{W},\mathbf{c},R}{\min} \sum\nolimits^{K}_{k=1} [ R^{2}_{k} + \frac{1}{vN}\sum\nolimits^{N}_{i=1}\max{0, \alpha_{ik}(||f(x_{i};\mathcal{W}) - \mathbf{c}_{k} ||^{2} - R^{2}_{k} ) } ], \end{equation} where class $k$ is specified by the distance from its center $\mathbf{c}_{k}$ and the radius $R_{k}$. An important point in \eqref{eq:softmcdd} is the class assignment indicator $\alpha_{ik}$, where it is 1 if $x_{i}$ belongs to class k, and -1 otherwise. The objective \eqref{eq:softmcdd} intuitively means to drag the within class samples to the corresponding sphere with center $\mathbf{c}_{k}$ and radius $R_{k}$, while pushing away other class samples from the sphere. This objective is named soft-boundary Deep-MCDD, which is denoted ‘Soft MCDD’ in the experiments.
Deep MCDD
The authors further introduce an alternative objective that learns Gaussian distribution, instead of hyperspheres. Assuming that the samples of class $k$ can be generated from an isotropic Gaussian distribution $\mathcal{N}(\mu_{k}, \sigma^{2}_{k}I)$ in the latent space without overlapping, the distance function $D_{k}(\cdot)$ based on the $k$-th class-conditional distribution is defined as: \begin{align} D_{k}(x) &= -\log P(x|y=k) \\ &= -\log \mathcal{N}(f(x;\mathcal{W})|\mu_{k}, \sigma^{2}_{k}I) \\ &\approx \frac{||f(x;\mathcal{W})-\mu_{k}||^{2}}{2\sigma^{2}_{k}} + \log \sigma^{d}_{k}. \label{eq:distance} \end{align} Now that the distance function is defined, the objective can be formulated as:
\begin{equation}\label{eq:deepmcdd} \underset{\mathcal{W},\mathbf{c},\sigma,b}{\min} \frac{1}{N} \sum\nolimits^{N}_{i=1} [ D_{y_{i}}(x_{i}) - \frac{1}{v} \log \frac{\exp(-D_{y_{i}}(x_{i})+b_{y_{i}})}{\sum^{K}_{k=1} \exp (-D_{k}(x_{i})+b_{k})} ]. \end{equation} The $v$ is a hyperparameter that determines the strictness of each hypersphere in both \eqref{eq:softmcdd} and \eqref{eq:deepmcdd}.
With the proposed distance function \eqref{eq:distance} and training objective \eqref{eq:deepmcdd}, multi-class ID classification and OOD detection can now be done by training a deep neural network with the final layer replaced by the distance metric layer defined as $-D_{k}(x) +b_{k}$. The objective \eqref{eq:deepmcdd} is denoted ‘Deep MCDD’ in the experiments.
Derive theoretical relationship between the proposed method and the Gaussian discriminant analysis
The authors derive theoretical relationship between the Deep MCDD \eqref{eq:deepmcdd} and the Gaussian discriminant analysis (GDA). The derivation begins by recalling the assumption of the GDA, where each class-conditional distribution follows multivariate Gaussian distribution ($P(x|y=k) = \mathcal{N}(f(x)|\mu_{k}, \Sigma_{k})$) and the class prior follows Bernoulli distribution ($P(y=k) = \frac{\beta_{k}}{\Sigma_{k^{\prime}} \beta_{k^{\prime}}}$). With a further assumption that each class covariance $\Sigma_{k}$ is isotropic, the posterior probability can be described as: \begin{align}\label{eq:posterior} P(y=k|x) &= \frac{P(y=k)P(x|y=k)}{\Sigma_{k^{\prime}} P(y=k^{\prime})P(x|y=k^{\prime})} \\ &= \frac{\exp (-(2\sigma^{2}_{k})^{-1} ||f(x)-\mu_{k}||^{2} - \log \sigma^{d}_{k} + \log\beta_{k})}{\Sigma_{k^{\prime}} \exp (-(2\sigma^{2}_{k^{\prime}})^{-1} ||f(x)-\mu_{k^{\prime}}||^{2} - \log \sigma^{d}_{k^{\prime}} + \log\beta_{k^{\prime}})}. \end{align} It can be seen that the second term of the \eqref{eq:deepmcdd} is equivalent to the posterior probability of GDA if the $\beta$ is considered as the bias $b$. To further relieve the assumption of the class-conditional distribution as the Gaussian distribution, which is usually not the case for the optimization of the deep neural network by stocahstic gradient descent, the authors show that minimizing Kullback-Leibler (KL) divergence between the the empirical class-conditional distribution and the Gaussian distribution also suffices.
Demonstrate performance of the proposed method quantitatively and qualitatively
The authors first compare the proposed objective with the softmax classifier and the Mahalanobis distance based classifier on tabular datasets.
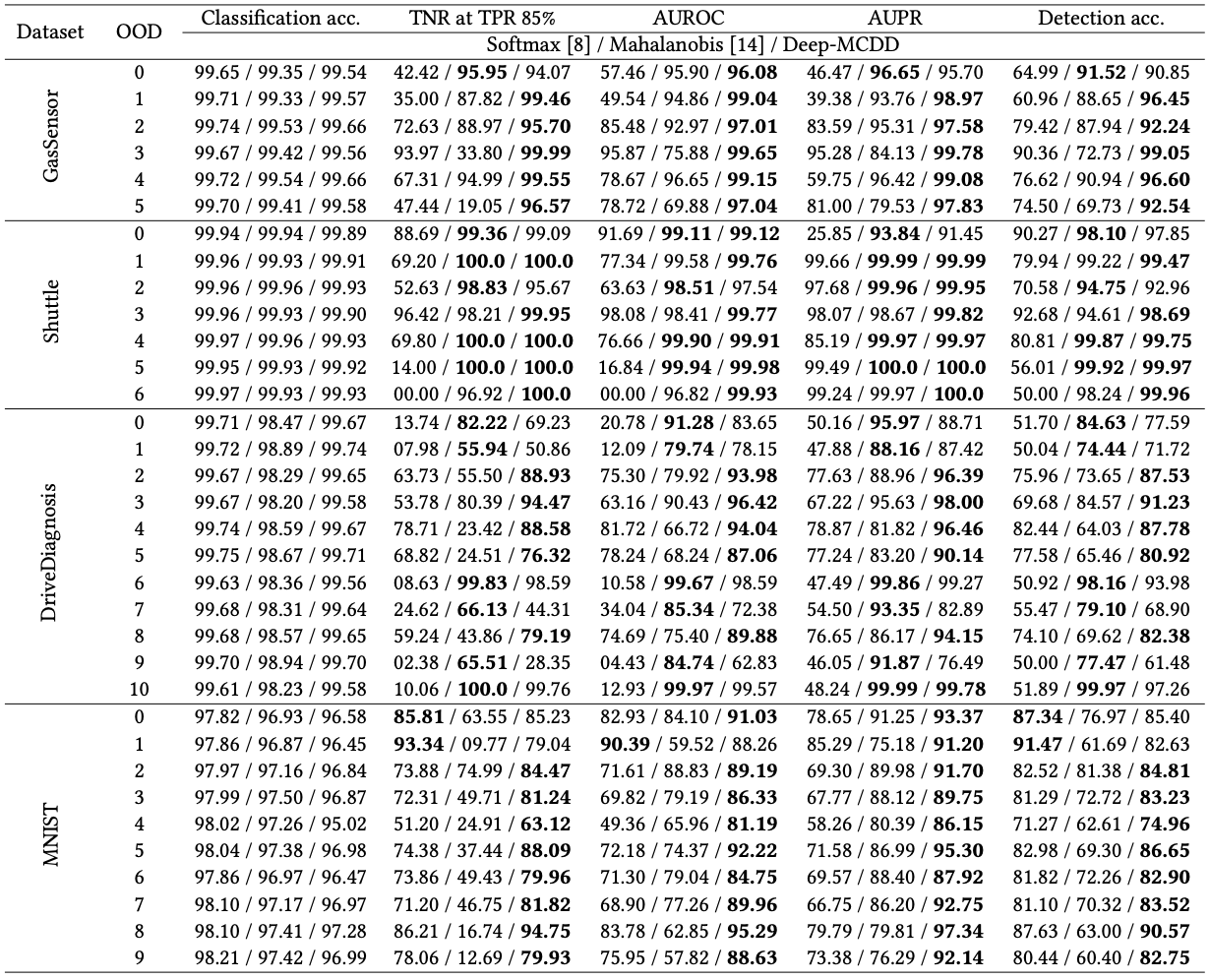Tabular data performance on ID classification and OOD detection
The qualitative result of the tabular data is demonstrated early in the Background section by the t-SNE latent space plot figure.
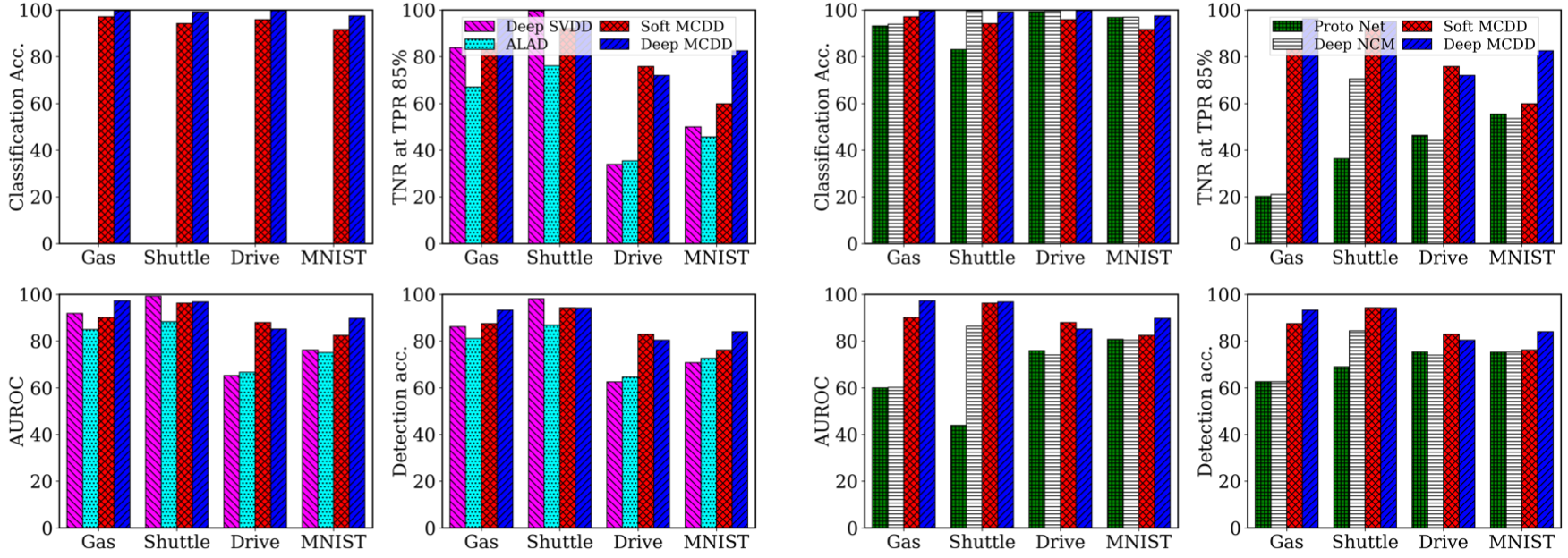Performance comparison with non-classifier-based OOD detectors and distance classifiers
The performance of ID classification and OOD detection on image data is also demonstrated.
ID classification performance on image datasets
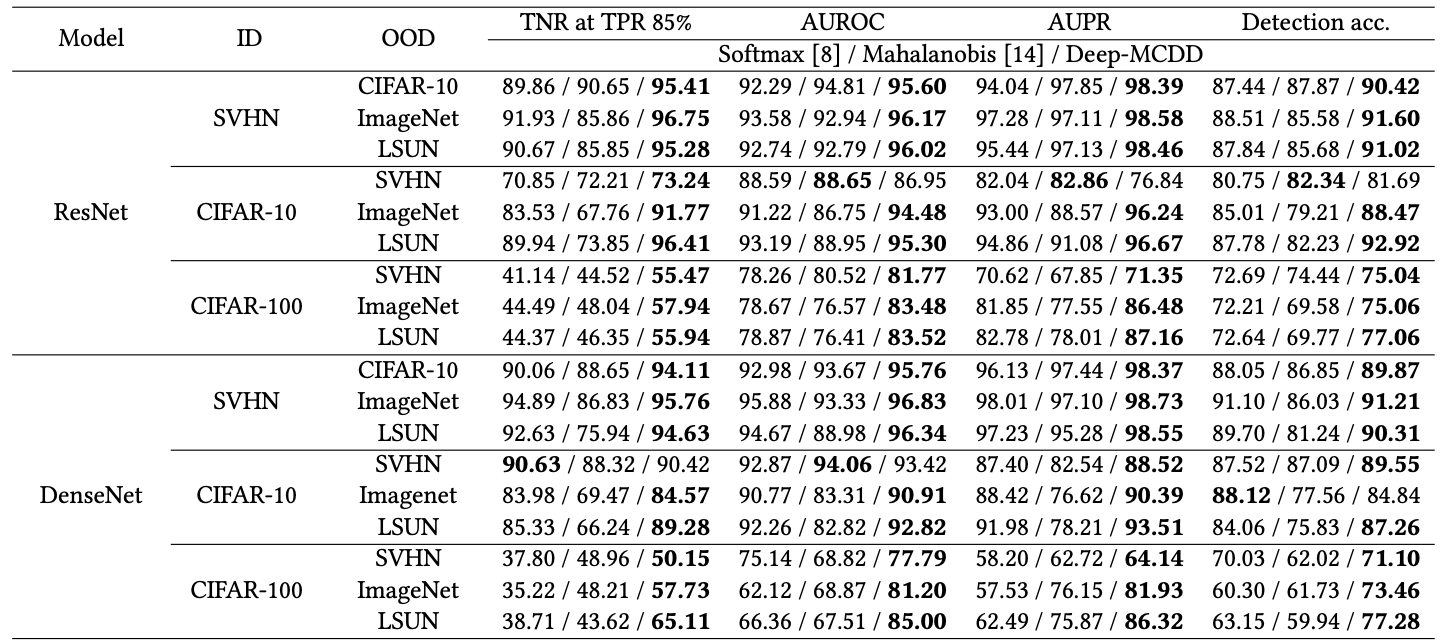OOD detection performance on image datasets