Significance
Keypoints
- Propose a method to learn the blur operator family
- Experimentally show performance on deblurring and blur synthesis while confirming their background theory
Review
Background
Deblurring is one of a typical ill-posed inverse problem that can be defined as \begin{equation}\label{eq:inv} y = \hat{\mathcal{F}}(x, k) + \eta \approx \hat{\mathcal{F}}(x, k), \end{equation} where $x$ is a clean image, $y$ is a corresponding blurry image, $\hat{\mathcal{F}}(\cdot, k)$ is the blur operator with the blur kernel $k$, and $\eta$ denotes the noise. Many conventional methods for deblurring focus on modeling the kernel $k$, with a simple assumption that the blur operator $\hat{\mathcal{F}}(\cdot, k)$ being the convolution function. Recent application of deep learning to the inverse problem have alternatively tried to solve this inverse problem by training a deep neural network $\mathcal{H}$ without considering the kernel $k$ and the kernel function $\hat{\mathcal{F}}(\cdot, k)$, \begin{equation}\label{eq:dnn} \hat{x} = \mathcal{H}(y), \end{equation} where $\hat{x}$ is the deblurred image of $y$. Although this approach has shown promising results, an important limitation still exists in that these methods often fail to generalize on an out-of-domain data that includes unseen blur operation during training. The authors propose to address these issues and propose a method that learns to encode the blur kernel and the blur operator from the clean-blurry image pairs $(x,y)$ with a deep neural network. Since the blur kernel and the blur operator are explicitly approximated with a neural network, generating realistic blur images can be done with the proposed method, not only the deblurring of clean images.
Keypoints
Propose a method to learn the blur operator family
The goal of the proposed method is to learn a blur operator family $\mathcal{F}$ that models the blur between the training dataset of $n$ data pairs ${(x_{i},y_{i}) }^{n}_{i=1}$.
A key idea is that the blur kernel $k_{i}$ between the image pairs of index $i$ can be approximated by training a kernel extractor $\mathcal{G}$ such that
\begin{equation}
k_{i} = \mathcal{G}(x_{i}, y_{i}).
\end{equation}
Now we can reformulate the right-hand-side of the inverse problem \eqref{eq:inv} as $\mathcal{F}(x_{i}, y_{i})$ to follow the left-hand-side of the \eqref{eq:inv} as $y_{i}$.
Specfically, the authors propose to minimize the following loss function, which can train $\mathcal{F}$ and $\mathcal{G}$ jointly:
\begin{equation}
\sum\nolimits^{n}_{i=1} \rho (y_{i}, \mathcal{F}(x_{i}, \mathcal{G}(x_{i},y_{i}))),
\end{equation}
where $\rho$ is the Charbonnier loss function (as in LapSRN).
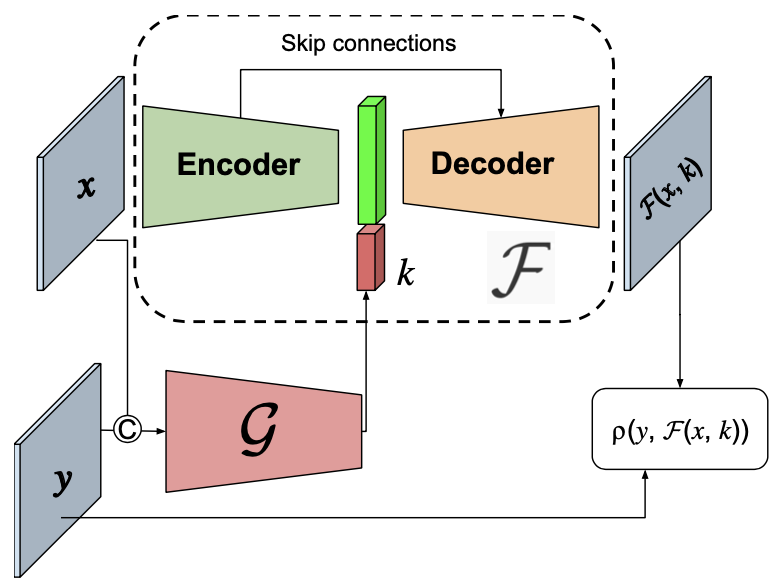Blur operator $\mathcal{F}$ and kernel extractor $\mathcal{G}$ are jointly trained
The authors further propose to reparametrize $x$ and $k$ with Deep Image Prior, add L2 regularization of the $k$, and use Hyper-Laplacian prior on image gradients of $x$ to stabilize the optimization.
Pseudocode of the final blind image deblurring process
Experimentally show performance on deblurring and blur synthesis while confirming their background theory
Now that the blur operator $\mathcal{F}$ and the kernel extractor $\mathcal{G}$ can be trained, experiments are needed to confirm this algorithm with a theoretical ground. The strength of this work includes that the authors show the generalization capability of the proposed method by training and testing their model on a separate benchmark dataset, the REDS and the GOPRO.
Blur kernel extractor experiments
The experiment starts on investigating whether the proposed method actually learns the blur kernel operator between the image pairs $(x,y)$.
This model was trained with the Levin dataset, which the blur kernel and the operator are already known.
The trained model is applied to the REDS and the GOPRO dataset to output the blur image.
The model output image was quantitatively compared with the ground-truth blur image, which the known blur kernel operator was applied.
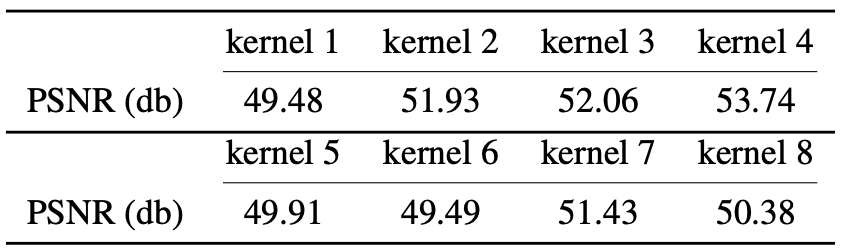Blur kernel operator is estimated well
Next, the blur image of the REDS and the GOPRO are swapped with the blur images inferred with the proposed method.
Training the SRN-Deblur model on the synthetic blur-swapped dataset achieves comparable performance with the real dataset.
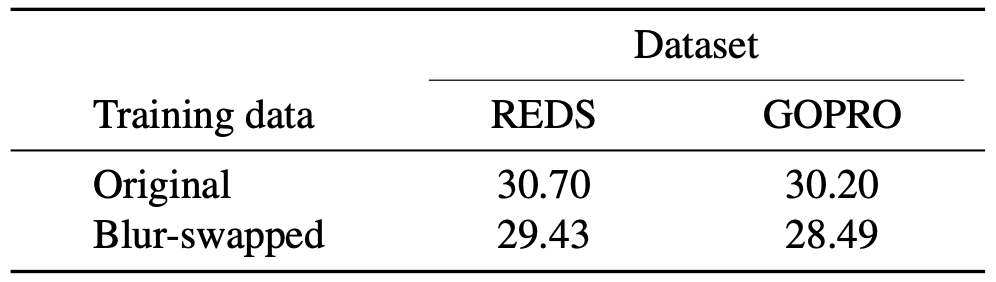Blur-swap dataset shows comparable result
Blind image deblurring experiments
Next, the general blind deblurring was performed on the REDS and the GOPRO dataset as the train and the test dataset, respectively.
The results suggest that the proposed methods qualitatively outperform previous methods including the DeblurGANv2, SRN-Deblur, and SelfDeblur.
Blind deblurring result with LPIPS(↓) values
Although the proposed method seems qualitatively better, it would have been better if the mean value of the LPIPS for the whole dataset were provided for each model.
Blur synthesis
The authors test the proposed method in terms of its capability in blur synthesis.
One application of the blur synthesis is the data augmentation during training a deep neural network based deblurring model as in \eqref{eq:dnn}.
The authors train the SRN-Deblur model with (i) common image augmentation (imgaug) and (ii) further blur synthesis augmentation of the proposed method combined (comb.) to show that the “comb.” results in improvement of quantitative performance of the final model.
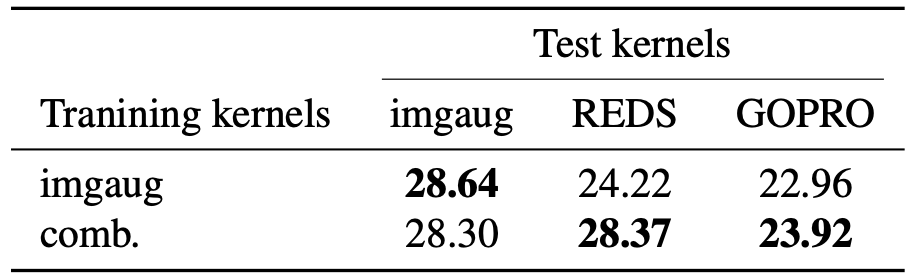Data augmentation with proposed method
This paper demonstrated a very interesting work which is theoretically sound, supported by experiments, with improvement in performance confirmed in a separate train-test dataset. I would personally say that the most disappointing aspect of this work is that it lacks a cool abbreviation of the proposed method. It would also be interesting to replace the encoder-decoder structure of the blur kernel operator to a conditional invertible neural network, which can directly invert the estimated blur image to the clean image without time-consuming optimization process.