Significance
Keypoints
- Propose an image processing method based on latent space optimization
- Demonstrate performance of the proposed method on RAW burst super-resolution and denoising
Review
Background
Image processing problems can be formulated as an ill-posed inverse problem $X = HY$ where $X$ is the observation, $Y$ is the original image, and $H$ is the image degradation. Accoerdingly, most image processing methods try to find the maximum a posteriori (MAP) estimate in the image domain: \begin{equation}\label{eq:map} \hat{y} = \underset{y}{\arg \min}\sum^{N}_{i=1} || x_{i} - H(\phi_{m_{i}}, (y))||^{2}_{2} + \mathcal{R}(y), \end{equation} where $i$ is the index of the multi-frame image, $\mathcal{R}(y)$ is the imposed regularization, and $\phi_{m}$ is the scene motion. However, the MAP formulation \eqref{eq:map} has limitations when employed to real-world settings. For example, it is assumed that the degradation operator $H$ is known, which is not usually true. The authors propose to reparameterize \eqref{eq:map} to minimize the distance between the target and the observation in the latent space by training an encoder $E$, a decoder $D$ and a degradation model $G$: \begin{equation}\label{eq:reparam} L(z) = \sum^{N}_{i=1} || E(x_{i}) - G(\phi _{m _{i}}(z))||^{2}_{2} + \mathcal{R}(D(z)) \end{equation} where $z$ is the latent vector and $G = E \circ H \circ D$.
Keypoints
Propose an image processing method based on latent space optimization
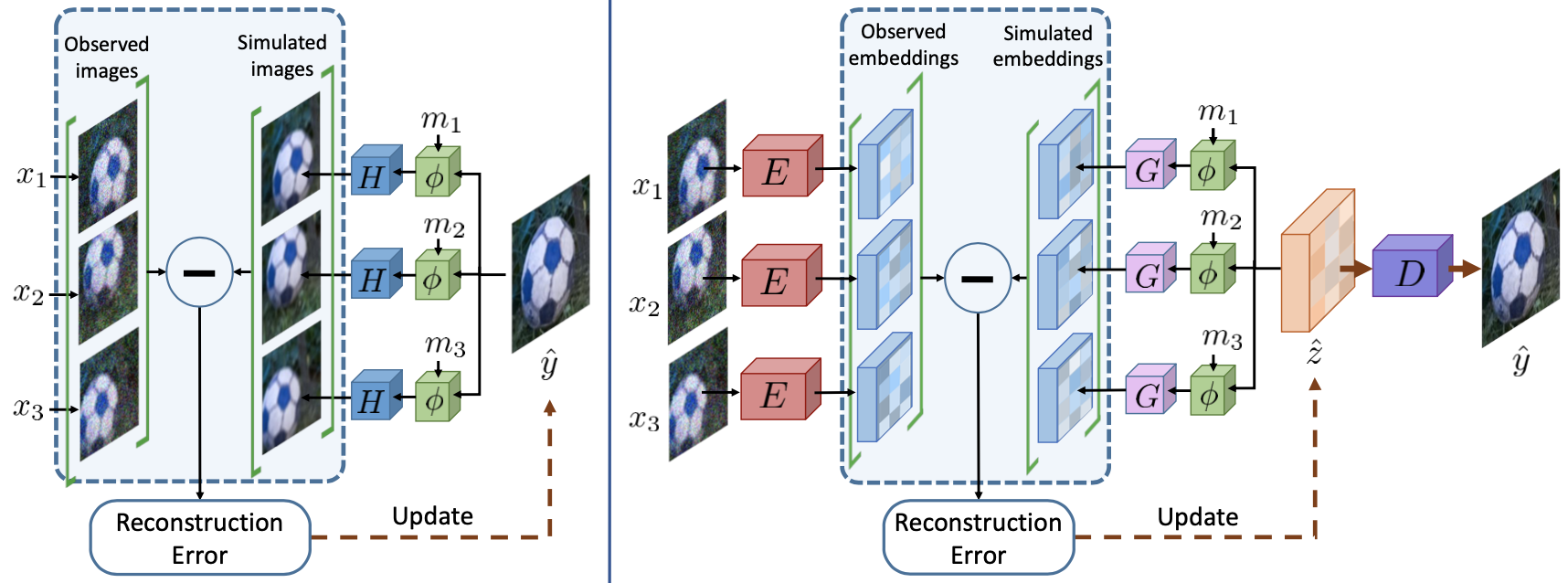Conventional MAP optimization \eqref{eq:map} (left) and the proposed reparameterization \eqref{eq:reparam} (right)
The training process of the proposed reparameterization \eqref{eq:reparam} is illustrated on the right side of the above figure.
The key part of the reparameterization is that the reconstruction error (distance between the observation and the target) is computed in the encoder-learned latent space.
The authors further employ certainty prediction and simplify regularization to be performed directly in the latent space to minimize:
\begin{equation}
L(z) = \sum^{N}_{i=1} || v_{i} \dot (E(x_{i}) - G(\phi _{m _{i}}(z)))||^{2}_{2} + \lambda ||z||^{2}_{2}
\end{equation}
where $\lambda$ is the regularization coefficient and $v_{i} = W({ E(x_{j}) }^{N}_{j=1},m_{i}, n_{i} )$ determines element-wise certainty values for modelling variable degradation in a single image with a function $W$.
Demonstrate performance of the proposed method on RAW burst super-resolution and denoising
The proposed reparameterization is applied to and experimented on RAW-to-RGB burst super-resolution and denoising tasks (ZRR, SyntheticBurst, BurstSR datasets).
Qualitative result on burst super-resolution (left) and denoising (right) tasks
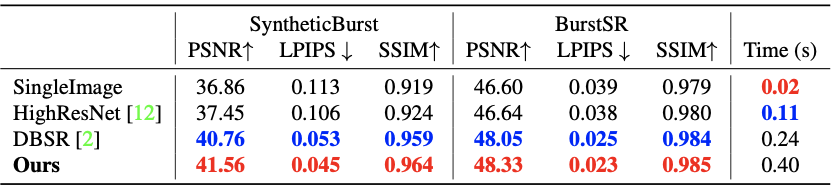Quantitative result on burst super-resolution task
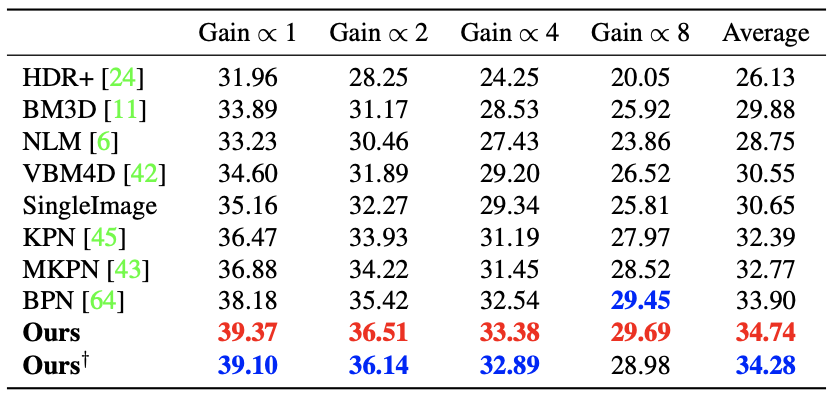Quantitative (PSNR) result on burst denoising task (grayscale)
Quantitative (PSNR) result on burst denoising task (color)
It can be seen that the proposed method outperforms other previous state-of-the-art burst super-resolution and denoising models both qualitatively and quantitatively.
Further ablation study results are referred to the original paper.