Significance
Keypoints
- Provide observation that blur amplification is harder for clean images
- Propose (self-)supervised algorithms for deblurring based on the observation
- Demonstrate perceptual performance of the proposed method
Review
Background
Learning based methods have been successfully applied to solving inverse problems in recent years, providing substantial improvement to the image processing tasks such as deblurring, denoising, etc.
Early learning based methods focused on improving the quantitative metrics (PSNR, SSIM) by minimizing the L1 or L2 distance between the target image and the input image.
However, the perception-distortion tradeoff suggests that higher PSNR does not necessarily mean better perceptual quality.
Most image processing algorithms now also consider whether the output image is perceptually better, often evaluated by LPIPS score or user response MOS.
The LPIPS score uses features of a trained CNN to infer whether the image is perceptually pleasing.
This feature of a trained CNN can also work as a loss function, known as perceptual loss, when the distance between the features are computed.
Minimizing the perceptual loss can often lead to better perceptual results, so many recent image processing models are trained with perceptual losses.
However, the authors question whether the specific problem of deblurring requires evaluating the high-level perceptual features of the input image.
Remaining blur of previous methods are amplified by reblurring
To address this issue, a new loss function is proposed for the deblurring task, while minimizing the loss can lead to perceptually better results.
This is made possible by the observation that the Clean Images are Hard to Reblur.
Keypoints
Provide observation that blur amplification is harder for clean images
The authors assume that a reblurring module $\mathcal{M}_{\text{R}}$, which amplifies the remaining blur of an image, will output an identical image to the input if there exists no blur in the input image.
To obtain the reblurring module, a blur reconstruction loss $\mathcal{L}_{\text{Blur}}$ is first proposed:
\begin{equation}
\mathcal{L}_{\text{Blur}} = ||\mathcal{M}_{\text{R}}(L) - B ||,
\end{equation}
where $L$ is a (non-ideally) deblurred image from the blurry image $B$.
The authors insist that this assumption is true by showing that higher deblurring PSNR corresponds to lower reblurring PSNR.
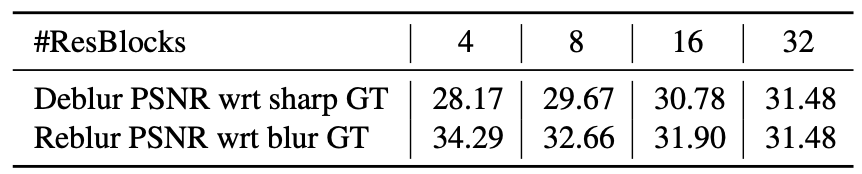Blur amplification is harder for clean images
Let $S$ be a sharp image corresponding to $B$. Going back to the first assumption, another objective function can be formulated between the sharp image $S$ and its output from the reblurring module $\mathcal{M}_{\text{R}}(S)$ become similar. The authors do not directly use the sharp image $S$ but exploit a deblurring module $\mathcal{M}_{\text{D}}$ to formulate the sharpness preservation loss $\mathcal{L}_{\text{Sharp}}$: \begin{equation} \mathcal{L}_{\text{Sharp}} = ||\mathcal{M}_{\text{R}}(\mathcal{M}_{\text{D}}(S)) - \mathcal{M}_{\text{D}}(S)||. \end{equation} The deblurring module can be any neural network based models.
Now, the reblurring module which provides a surrogate information for the authors’ observation can be trained with the following joint loss: \begin{equation} \mathcal{L}_{\text{R}} = \mathcal{L}_{\text{Blur}} + \mathcal{L}_{\text{Sharp}}. \end{equation}
Propose (self-)supervised algorithms for deblurring based on the observation
Reblurring loss
Now that the blurriness of the image can be evaluated by the reblurring module, a reblurring loss $\mathcal{L}_{\text{Reblur}}$ is defined as: \begin{equation} \mathcal{L}_{\text{Reblur}} = || \mathcal{L}_{\text{R}}(L) - \mathcal{L}_{\text{R}}(S)||. \end{equation} The deblurring module $\mathcal{M}_{\text{D}}$ can be trained by the conventional L1 loss along with the reblurring loss, which provides surrogate information about how much the blurriness is left in the deblurred image. This reblurring loss might seem similar to adversarial loss for adversarial training. However, the reblurring loss does not focus on high-level realism of the image but rather on the level of blurriness.
Self-reblurring loss
The training of deblurring module can also be performed in a self-supervised manner during test time.
This self-supervised algorithm is described in the following pseudocode.
Pseudocode of self-supervised test-time adaptation
Demonstrate perceptual performance of the proposed method
The experiments are performed on the GOPRO and REDS datasets.
Baseline deblurring models $\mathcal{M}_{\text{D}}$ included U-Net, SRN, and modified DM-PHN (DHN).
For the reblurring module, a simple ResNet with 1 or 2 ResBlocks are used.
The main evaluation is done over perceptual metrics, the LPIPS and the NIQE.
Experiment results indicate that the proposed methods provide significant improvement of perceptual metric scores of the deblurring modules.
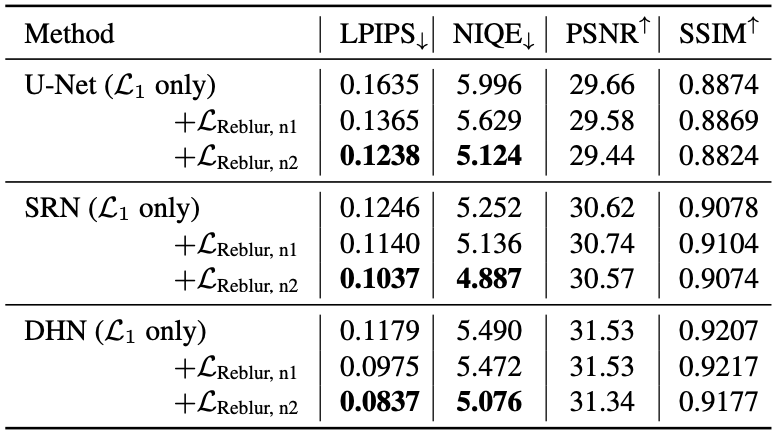GOPRO dataset results. n1 and n2 refer to number of ResBlocks
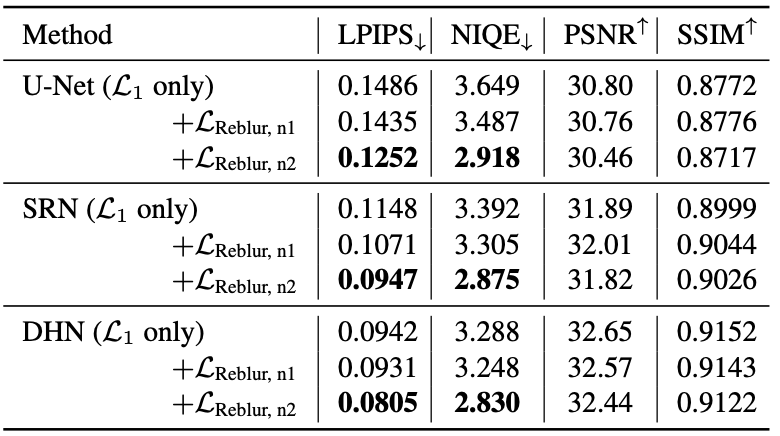REDS dataset results
The quantitative and qualitative results of the test time adaptation experiments also showed significant improvement of the metrics.
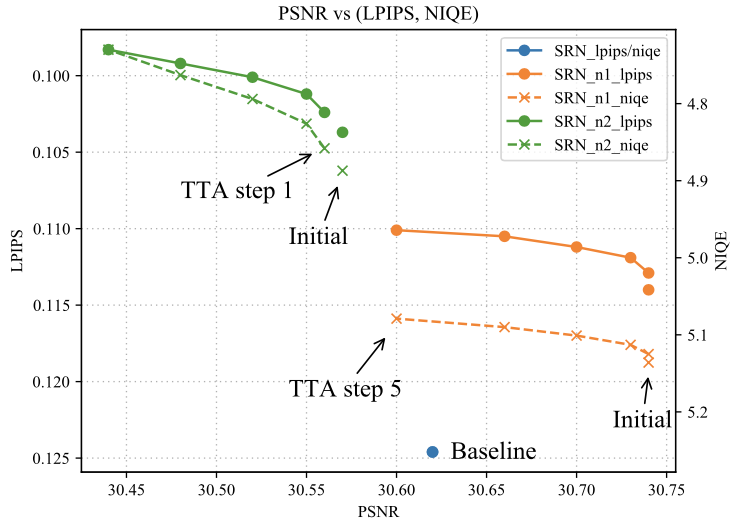Test-time adaptation result with SRN and GOPRO dataset
Qualitative results of the test-time adaptation
In short, the authors proposed a novel loss function based on an intuitive observation which led to significant improvement of perceptual performance of the deblurring models. Ablation and comparative studies are also available in the original paper.