Significance
Keypoints
- Propose a framework for learning image representation by combining generative and contrastive methods
- Demonstrate discriminative and generative performance of the proposed method
Review
Background
Learning representation with contrastive learning strategy based on augmentation, such as SimCLR, is shown to be effective for learning image representation without labels. While the performance of contrastive learning methods on downstream discriminative vision tasks are superior to the generative learning methods, generative methods have advantage in that they are more likely to be robust under distributional shift. The authors address this trade-off between the two unsupervised image representation learning regime and propose Generative-Contrastive Representation Learning (GCRL), a hybrid generative-contrastive framework.
Keypoints
Propose a framework for learning image representation by combining generative and contrastive methods
To combine the generative and contrastive methods, the objective $\mathcal{L}$ is defined from the generative objective $\mathcal{L}_{g}$ and the contrastive objective $\mathcal{L}_{c}$: \begin{align} \mathcal{L} &= \alpha \mathcal{L}_{g}+ \beta \mathcal{L}_{c}, \\ \mathcal{L}_{g} &= -\frac{1}{N}\sum^{N}_{i=1}\log p(\mathbf{x}_{i}^{(1)}) = -\frac{1}{N} \sum^{N}_{i=1}(\sum^{D}_{k=2}\log p (\mathbf{x}^{(1)}_{i,k} \mid \mathbf{x}^{(1)}_{i,<k})), \\ \mathcal{L}_{c} &= -\frac{1}{2N} \sum^{N}_{i=1} \Bigl( \log\frac{\exp(\frac{\mathbf{z}_{i}^{(1)}\cdot \mathbf{z}_{i}^{(2)} }{\tau})}{\sum_{j\neq i}\exp(\frac{\mathbf{z}^{(1)}_{i}\cdot \mathbf{z}^{(1)}_{j}}{\tau}) + \sum_{j}\exp(\frac{\mathbf{z}^{(1)}_{i}\cdot \mathbf{z}^{(2)}_{j}}{\tau})} + \log\frac{\exp(\frac{\mathbf{z}_{i}^{(2)}\cdot \mathbf{z}_{i}^{(1)} }{\tau})}{\sum_{j\neq i}\exp(\frac{\mathbf{z}^{(2)}_{i}\cdot \mathbf{z}^{(2)}_{j}}{\tau}) + \sum_{j}\exp(\frac{\mathbf{z}^{(2)}_{i}\cdot \mathbf{z}^{(1)}_{j}}{\tau})} \Bigr), \end{align} where $(\mathbf{z}_{i}^{(1)}, \mathbf{z}_{i}^{(2)})$ are representation vectors from the augmented image pairs (weak and strong) $(\mathbf{x}_{i}^{(1)}, \mathbf{x}_{i}^{(2)})$, $\alpha$, $\beta$ are coefficients of generative and contrastive loss, and $\tau$ is the temperature parameter of contrastive learning.
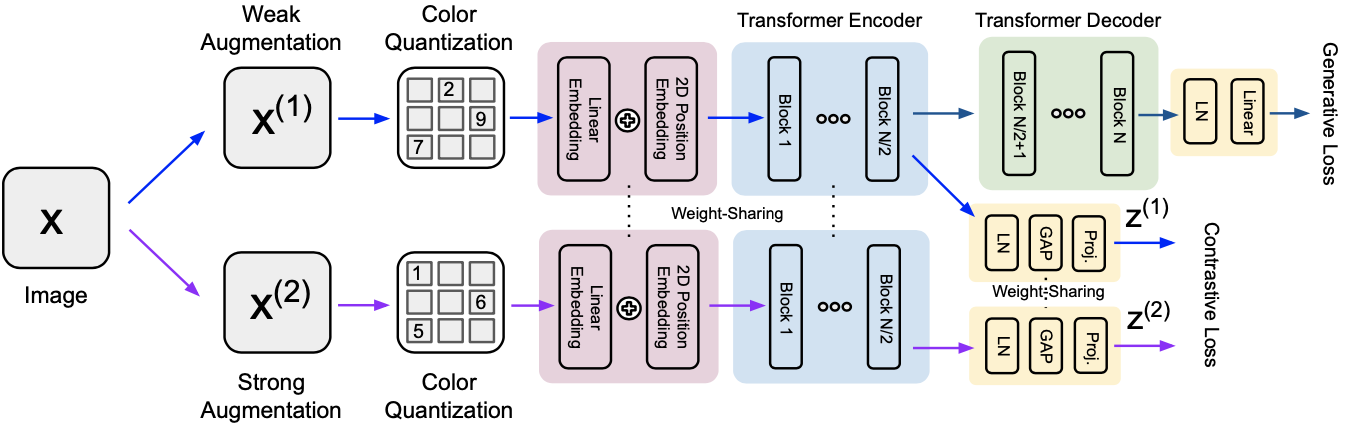Training scheme of GCRL
The model architecture follows iGPT with color quantization and AxialTransformer sparse attention for computational efficiency in each Transformer blocks. Later blocks are considered as the decoder part of the generative model.
Demonstrate discriminative and generative performance of the proposed method
Performance of GCRL is compared with baseline contrastive (SimCLR) and generative (iGPT) methods.
It can be seen from the experimental results that the GCRL is capable of learning representation with both discriminative and generative features.
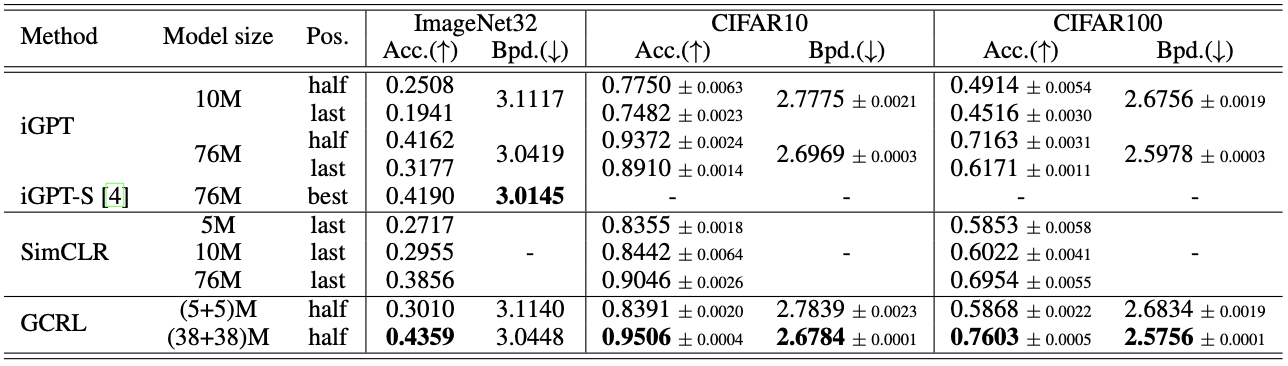Comparative study result of the proposed method
Qualitative comparison of the generated images trained on ImageNet is also provided, and the FID score is reported to be comparable to that of the iGPT.
Qualitative result of image generation with GCRL (right), compared to iGPT (left)
Importantly, the robustness on out-of-distribution (OOD) samples are experimented in both supervised and unsupervised settings.
The OOD detection results show that the GCRL achieves at least comparable performance when compared to the generative model iGPT.
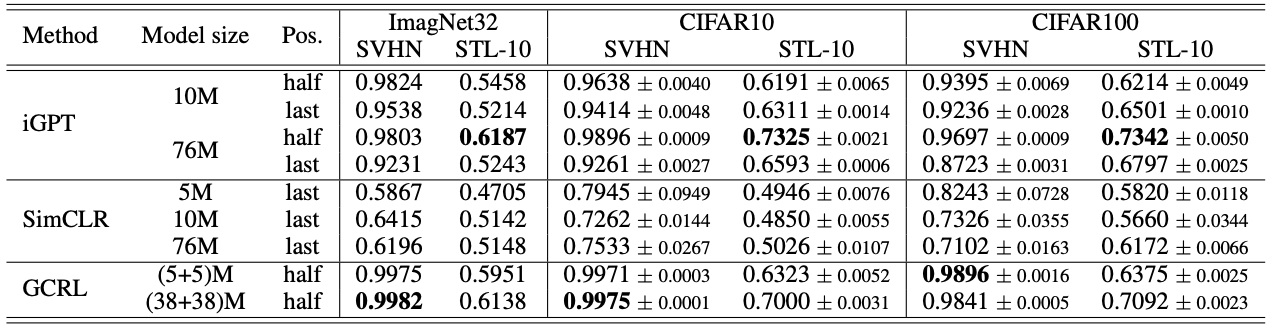Supervised OOD detection task result
Unsupervised OOD detection task result
It is suggested from the experiments that the GCRL takes advantage of both discriminative and generative pre-training methods. Ablation study results are referred to the original paper.