Significance
Keypoints
- Propose a unifying framework for data subset selection by introducing submodularity
- Demonstrate subset selection result from experiments
Review
Background
When selecting a subset of samples from a full dataset, there may exist a selection which has the ideal distribution.
Here, the ideal distribution refers to the distribution of selected samples that leads to better performance over other selections when used for training a model.
Most previous methods that try to select the best subset focus on some notion of margin, representativeness, or diversity.
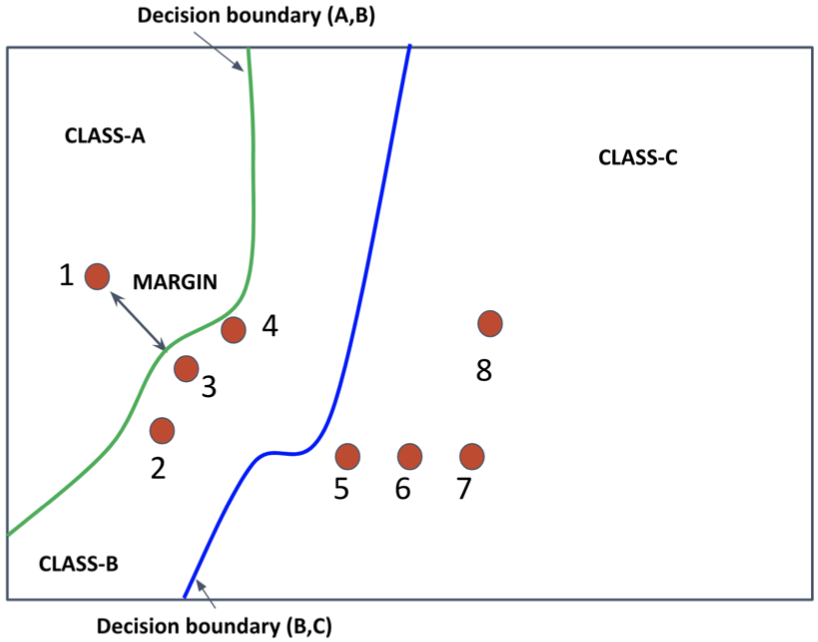An exemplar plot of decision boundaries and training samples in the latent space
From the above figure, the margin refers to how close the training sample lies to a decision boundary.
The closer the sample is, the more uncertain the decision is.
It can be said that the set of samples {2,3,4} has higher uncertainty than the set {1,3,7}.
The representativeness refers to whether the sample can represent other data from the same class.
It can be said that the set of samples {3,6} imply more representativeness on class B and C than {1,8} does on class A and C.
Lastly, the diversity refers to whether the set includes samples from a more diverse class.
It is straightforward that {1,3,7} has greater diversity than {2,3,4} or {5,6,7}.
Before unifying these three concepts into one algorithm, the authors formulate the data subset selection problem into a combinatorial optimization problem subject to a set function $f:2^{G} \rightarrow \mathbb{R}$, where every subset of the dataset $G$ is mapped to a real value indicating the utility value (how much it is worth selecting). Finding an optimal solution from the discrete space with $2^{G}$ elements is not computationally friendly. So, the authors take some steps to make this optimization problem tractable: (i) reduce the domain of the discrete space to $S$ by applying constraints to $G$ where $|S|<|G|$, (ii) formulate $f$ to be a submodular set function, (iii) apply greedy algorithm to find optimal subset of $S$. Here, (ii) and (iii) are closely related. A submodular set function can be thought of a convex function in the discrete space, and a greedy algorithm is applied to find a solution of our interest efficiently.
For more information on submodularity, visit submodularity.org for excellent tutorials and materials
Keypoints
Propose a unifying framework for data subset selection by introducing submodularity
Our goal is to find the optimal subset $S^{\ast}$ by solving: \begin{equation} S^{\ast} = \underset{S \subseteq G}{\arg\max}, \quad \text{s.t.} |S| = k, \end{equation} where $k$ is the budget that decides how many data samples should be selected. The function $f$ is a conic combination of four submodular functions \begin{equation} f(S) = \lambda_{1}f_{\text{uncertainty}}(S) + \lambda_{2}f_{\text{diversity}}(S) + \lambda_{3}f_{\text{triple}}(S) + \lambda_{4}f_{\text{mmd}}(S), \end{equation} where $\lambda_{i} \geq 0, i \in \{1,2,3,4\}$ so the function $f$ is also submodular. The $f_{\text{uncertainty}}(S)$ is related to the margin, $f_{\text{mmd}}(S)$ is related to the representativeness, and $f_{\text{diversity}}(S)$, $f_{\text{triple}}(S)$, $f_{\text{mmd}}(S)$ are related to the diversity.
Function: Uncertainty
The uncertainty function $f_{\text{uncertainty}}(S)$ is defined as \begin{equation} f_{\text{uncertainty}}(S) = \sum_{i\in S}u(i), \end{equation} where the utility function $u(i)$ corresponds to the difference in class probability between the best predicted class $bb$ and the second best predicted class $sb$ from a model trained with a small fraction (10\% in this paper) of the available training dataset: \begin{equation} u(i) = 1 - (P(Y=bb|x_{i})-P(Y=sb|x_{i})). \end{equation}
Function: Diversity
The diversity function $f_{\text{diversity}}(S)$ is defined as: \begin{equation} f_{\text{diversity}}(S) = \sum_{i \in S}\text{unary}(i) - \gamma \sum_{i,j:(i,j) \in E,\quad i,j \in S} s(i,j), \end{equation} where the pairwise similarity $s$ is the cosine distance and the unary function is $\text{unary}(i)=\max _{l \in G} \sum_{j:(l,j) \in E} s(l,j)$ to capture the utility of an individual image while ensuring monotonicity.
Function: Triple
The clique function $f_{\text{triple}}$ refers to the area of the triangle spanned by degree 3 cliques $\mathcal{T}$ from a graph defined by nearest neighbor: \begin{equation} f_{\text{triple}}(S) = \sum_{i \in S}\alpha (i) - \eta \sum\nolimits_{i,j,k: (i,j,k) \in \mathcal{T}, \quad i,j,k\in S } t(i,j,k), \end{equation} where $\alpha (i)$ is the number of triple cliques involving sample $i$, and $t(i,j,k)$ is an indicator function being 1 when the area of the triangle (i,j,k) is under certain threshold and 0 otherwise. Maximizing $f_{\text{triple}}$ means to prefer triplet of samples that consume larger area in the latent space.
Function: Maximum Mean Discrepancy (MMD)
The MMD function comes from this paper, and is defined as: \begin{equation} f_{\text{MMD}}(S) = \sum\nolimits_{i\in S}\sum\nolimits_{j:(i,j)\in E} s(i,j) - \xi \sum\nolimits_{i,j: (i,j)\in E, i,j\in S} s(i,j). \end{equation} The first term promotes preference to images with high connectivity, while the second term promotes diversity.
Proofs that above four functions are submodular and monotonically non-decreasing are referred to the original paper.
Constraints: Class balancing and Boundary balancing
We have discussed about the step (ii) and the step (iii) that was mentioned in the background session, but not step (i). The step (i) is to reduce the domain $G$ by applying constraints. Two constraints that the authors propose are the class balancing constraint and the boundary balancing constraint. The details of the two constraints will not be covered in this review, but the motivations are as follows. The class balancing constraint refers to selecting subset of the dataset that class imbalance of samples (some class having many samples while others do not) is hard to occur. The boundary balancing constraint is to select samples that are close to the decision boundary.
Unifying subset selection
Now, the subset selection is given by:
\begin{equation}
S^{\ast} = \underset{S \subseteq G}{\arg \max} f(S), \quad \text{s.t.} |S|=k, S\in\mathcal{I}_{c}, S\in\mathcal{I}_{d},
\end{equation}
where $\mathcal{I}_{c}$ and $\mathcal{I}_{d}$ are class balancing and boundary balancing constraints, respectively.
The greedy algorithm is used for selecting the subset of size $k$.
The greedy algorithm
Demonstrate subset selection result from experiments
Subset selection performance is experimented over four datasets for image classification: CIFAR-10, CIFAR-100, ImageNet, and CIFAR-100-LT (Long-tailed with class imbalance) with ResNet-56 model.
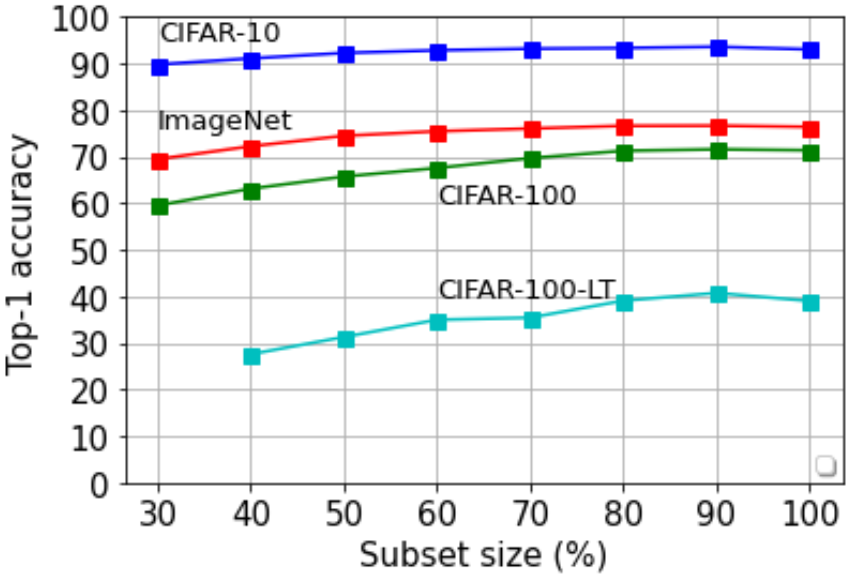ResNet-56 on subset data selected with proposed method
Comparison with other baseline selection methods (random, margin, diversity, k-ctr) showed that the proposed method outperforms under most budget $k$ settings.