Significance
Keypoints
- Parameterize distribution of adversarial examples in a continuous space
- Demonstrate performance of the proposed adversarial attack in terms of successful attack and semantic similarity
Review
Background
Adversarial sample refers to a data that is perceptual similar to the original sample, but a trained model $h$ fails to classify it.
Existing methods for creating adversarial samples often exploit optimization-based search strategies for image or speech data.
However, optimization with gradient descent is usually not possible for text data, which is discrete in nature.
The authors mitigate this issue by approaching the adversarial attack as sampling from adversarial distribution rather than perturbing each discrete input tokens.
This not only allows us to optimize the adversarial distribution with gradient descent, but also add soft constraints that can preserve fluency or semantic similarity.
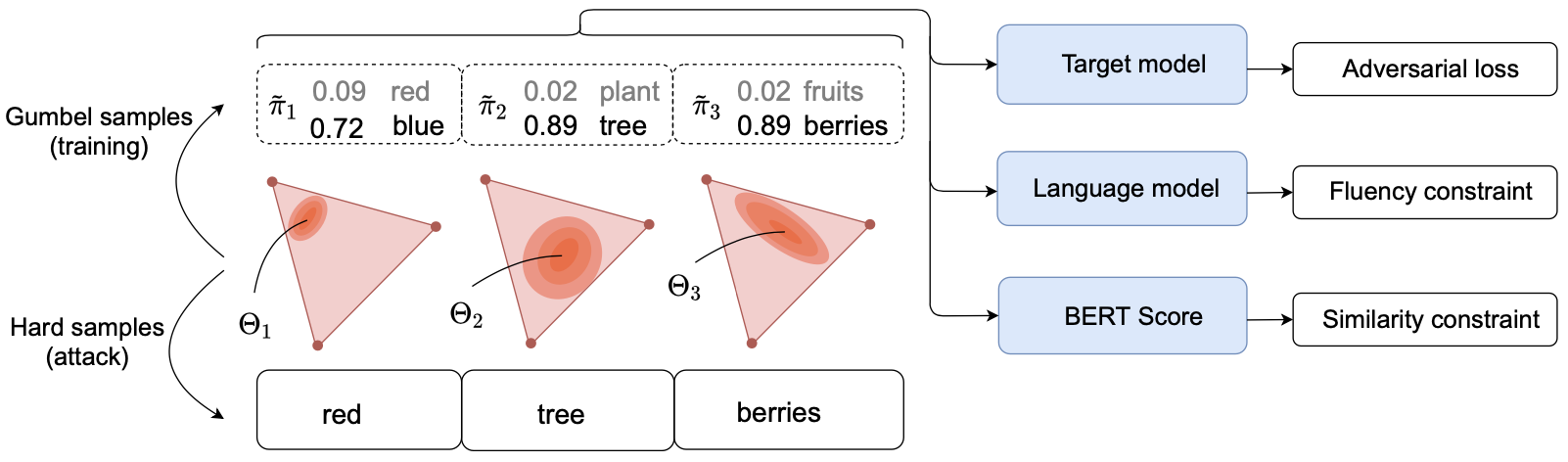Schematic illustration of the proposed method
Keypoints
Parameterize distribution of adversarial examples in a continuous space
Let $\mathbf{z}$ be a sequence of word tokens $z_{1}z_{2}\cdots z_{n}, z_{i} \in \mathcal{V}$ where $\mathcal{V}$ is a fixed vocabulary $\mathcal{V}={1,…,V}$. A distribution $P_{\Theta}$ parameterized by $\Theta \in \mathbb{R}^{n\times V}$ can be considered, which the samples can be drawn from $\mathbf{z} \approx P_{\Theta}$ by sampling each token from \begin{equation} \label{eq:discrete_distribution} z_{i} \approx \text{Categorical}(\pi_{i}) \end{equation} where $\pi_{i}$ refers to the softmax probability vector of $\Theta_{i}$. The objective is to find the solution of: \begin{equation}\label{eq:objective} \underset{\Theta}{\min}\mathbb{E}_{\mathbf{z}\approx P_{\Theta}}l(\mathbf{z},y;h), \end{equation} where $l$ is the adversarial loss. Since \eqref{eq:objective} is not differentiable becuase of the categorical distribution in \eqref{eq:discrete_distribution}, the authors propose to (i) extend the model $h$ to take probability vectors as input and (ii) use the Gumbel-softmax for approximating the gradient.
Probability vectors as input
Input to a transformer based model $h$ usually is an embedding $\mathbf{e}(z_{i})$ which the one-hot token $z_{i}$ is converted with an embedding function $\mathbf{e}(\cdot )$. The authors compute dot product between the probability vector $\pi_{i}$ and the embedding vector: \begin{equation} \mathbf{e}(\pi_{i})=\sum\nolimits_{j=1}^{V}(\pi_{i})_{j}\mathbf{e}(j). \end{equation} Now the probability distribution can be used as an input to the model $h$.
Computing gradient with Gumbel-softmax
The extension of the model $h$ to take probability distribution enables Gumbel-softmax approximation of the gradient of \eqref{eq:objective}. Samples $\tilde{\mathbf{\pi}}=\tilde{\pi_{1}} \cdots \tilde{\pi_{n}}$ are drawn from the Gumbel-softmax distribution $\tilde{P}_{\Theta}$: \begin{equation} (\tilde{\pi}_{i})_{j} := \frac{\exp((\Theta_{i,j}+g_{i,j})/T)}{\sum^{V}_{v=1}\exp((\Theta_{i,v}+g_{i,v})/T)}, \end{equation} where $g_{i,j} \approx \text{Gumbel}(0,1)$ and $T>0$ is the parameter that controls smoothness of the function. Now the objective \eqref{eq:objective} can be reformulated as: \begin{equation} \underset{\Theta}{\min}\mathbb{E}_{\tilde{\mathbf{\pi}}~\tilde{P}_{\Theta}} l(\mathbf{e}(\tilde{\mathbf{\pi}}),y;h), \end{equation} where the parameter $\Theta$ can now be optimized with gradient descent! The margin loss function is used as the adversarial loss $l$ for training: \begin{equation} l_{\text{margin}}(\mathbf{x},y;h) = \max(\phi_{h}(\mathbf{x})_{y} - \underset{k\neq y}{\max}\phi_{h}(\mathbf{x})_{k} + \kappa,0). \end{equation}
Soft constraints
While optimizing the parameter $\Theta$ with the adversarial loss, other objectives that promote fluency or semantic similarity can be introduced loss function. The semantic similarity or fluency are often constrained by a hard-coded, non-differentiable process, so the authors propose soft constraints that can be optimized with gradient descent as an objective function. The soft fluency constraint uses auto-regressive causal language models (CLMs), and the soft similarity constraint uses distance between the BERTScore similar to the perceptual loss of image data.
Demonstrate performance of the proposed adversarial attack in terms of successful attack and semantic similarity
The adversarial attack was performed on various text classification datasets including DBPedia, AG News, Yelp reviews, IMDB, and MNLI for models including GPT-2, XLM, and BERT.
The adversarial accuracy was significantly lower than the clean accuracy while the cosine similarity of the USE embedding was well preserved.
Adversarial attack performance of the proposed method
The method was also evaluated qualitatively.
Successful adversarial examples of the proposed method (GBDA)
Other ablation and transfer attack setting experiments are extensively performed, but the results are referred to the original paper.