Significance
Keypoints
- Propose a transformer module which replaces dot product attention into element-wise multiplication
- Demonstrate performance and efficiency of the proposed method
Review
Background
Transformers employ dot-product between a sequence of query and key vectors to compute attention between each items in the sequence. This means that for a sequence of $T$ length $d$ query/key vectors, the computational complexity of attention $\mathcal{O}(T^{2}d)$ is quadratic to the sequence length. The authors propose attention free transformer (AFT), which maintains the interaction modeling of the Transformer while replacing the scaled dot-product attention into a new operation based on computationally efficient element-wise multiplication.
Keypoints
Propose a transformer module which replaces dot product attention into element-wise multiplication
The AFT is defined as:
\begin{align}\label{eq:aft}
\sigma_{q}(Q_{t})\odot \frac{\sum^{T}_{t^{\prime}=1}\exp(K_{t^{\prime}}+w_{t,t^{\prime}})\odot V_{t^{\prime}}}{\sum^{T}_{t^{\prime}=1}\exp(K_{t^{\prime}}+w_{t,t^{\prime}})},
\end{align}
where $t$ is the index of the sequence with length $T$, $\odot$ is the element-wise product, $\sigma_{q}$ is the nonlinearity (sigmoid), $w\in R^{T\times T}$ is the learnable position biases.
The proposed \eqref{eq:aft}, which is denoted AFT-full, replaces scaled dot-product attention of the Transformer with lower computational complexity.
Computational complexity of the proposed method and Transformer variants
The authors suggest variants of the AFT to achieve locality while further reducing the computational complexity. AFT-local refers to the AFT which the learnable position biases $w_{t,t^{\prime}}$ are set to zero when $t$ and $t^{\prime}$ are not within a certain local range: \begin{align} w_{t,t^{\prime}} = \begin{cases} w_{t,t^{\prime}}, &\text{if} |t-t^{\prime}|<s \\ 0, &\text{otherwise}, \end{cases} \end{align} where $s\leq T$ is the window size. The authors mention that AFT-local maintains global connectivity, but the definition of global connectivity was not apparent to me. AFT-simple is an extreme case of the AFT-local which the learnable position biases do not exit, i.e. set to zero. AFT-conv explicitly employs depth-wise separable convolution layer to the \eqref{eq:aft} which leads to better performance.
Demonstrate performance and efficiency of the proposed method
The performance and efficiency of the proposed method is demonstrated by experiments on image autoregressive modeling, language modeling, and image classification tasks.
For the image autoregressive modeling, the negative log likelihood on the CIFAR-10 test dataset is compared with baseline methods.
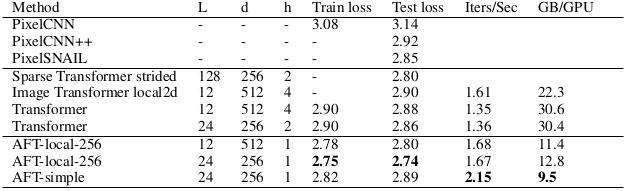Image autoregressive modeling result on CIFAR-10
It can be seen that the propose AFT-local and AFT-simple achieve better performance with low computational cost.
Language modeling performance is evaluated with the Enwik8 dataset, with the same negative log likelihood metric.
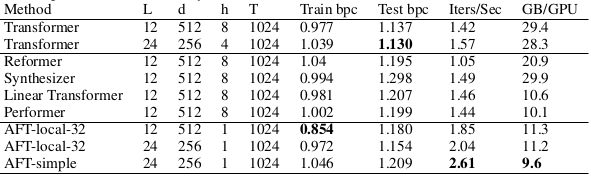Language modeling result on Enwik8
The test result show a comparable performance to the Transformer with faster computing time.
Results of the ablation/comparative study on window size $s$ and the sequence size $T$ are referred to the original paper
Lastly, image classification performance on ImageNet-1K dataset is evaluated.
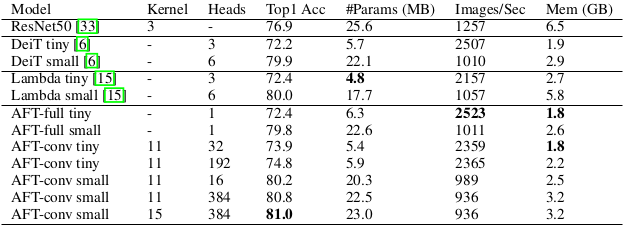Image classification result on ImageNet-1K
The proposed AFT variants achieve better performance with computational efficiency when compared to baseline models.
Another finding is that intializing some of the parameters of the AFT (value weight matrix, etc) from the pre-trained DeiT provide improvement in the image classification performance.