[2106.00132] On Fast Sampling of Diffusion Probabilistic Models

• Propose a framework for fast forward/inverse sampling in trained diffusion models
• Demonstrate performance of the proposed method in image and audio generation

Background

Diffusion models are recently gaining attention as the generative model that enables sampling high quality image or audio data from a known, simple distribution. The Denoising Diffusion Probabilistic Model (DDPM) is a $T$-step markov chain that learns to gradually denoise a noisy image at each step. Recent improvements in the diffusion models showed state-of-the-art image synthesis quality which even surpasses that of GANs (see my previous post for a review of the paper Diffusion Models Beat GANs on Image Synthesis). However, generating the high quality image from a random noise requires computing $T$ times of reverse process, which is very slow. Thus, acceleration of diffusion models can be of importance for the models to be practically available for solving real-world problems.

Keypoints

Propose a framework for fast forward/inverse sampling in trained diffusion models

The authors propose FastDPM, a method that accelerates the sampling process of the diffusion models by approximating the already trained DDPM with smaller number of steps $S \ll T$. This acceleration of FastDPM is based on (i) generalizing the discrete diffusion steps to continuous diffusion steps, and (ii) designing a bijective mapping between the continuous diffusion steps and the continuous noise level.

The noise level at step $t$ is defined as the $\mathcal{R}(t) = \sqrt{\bar{\alpha_{t}}}$, where $\bar{\alpha_{t}}= \Pi_{i=1}^{t}\alpha_{i}$, and $\alpha_{t}$ is from the equation $x_{t} = \sqrt{\bar{\alpha_{t}}}\cdot x_{0} + \sqrt{1-\bar{\alpha_{t}}}\cdot \epsilon$. $x_{t}$ is the noisy data at step $t$ and $x_{0}$ is the clean image. Extending the domain of $\mathcal{R}$ to real values is realized by exploiting the Gamma function $\Gamma$: \begin{align} \mathcal{R}(t) = (\Delta \beta)^{\frac{t}{2}}\Gamma(\hat{\beta}+1)^{\frac{1}{2}} \Gamma (\hat{\beta}-t + 1)^{-\frac{1}{2}}, \end{align} where $\{ \beta \}^{T}_{t=1}$ is the variance schedule, $\Delta \beta = \frac{\beta_{T}-\beta_{1}}{T-1}$, $\hat{\beta} = \frac{1-\beta_{1}}{\Delta \beta}$. For the noise level $r$, its corresponding step can be defined with the inverse of the mapping $\mathcal{T} = \mathcal{R}^{-1}$, or $\mathcal{T}(r) = \mathcal{R}^{-1}(r)$. By Sterling’s approximation of the Gamma functions: \begin{align} \label{eq:T} 2\log \mathcal{R}(t) = t\Delta \beta + (\hat{\beta}+\frac{1}{2})\log \hat{\beta} - (\hat{\beta} - t + \frac{1}{2})\log (\hat{\beta}-t)-t + \frac{1}{12}(\frac{1}{\hat{\beta}}-\frac{1}{\hat{\beta}-t}) + \mathcal{O}(T^{-2}). \end{align} The equation $t=\mathcal{T}(r)$ is numerically solved with a binary search based on \eqref{eq:T}.

Now, the bijective functions $\mathcal{T}$, $\mathcal{R}$ which maps continuous diffusion steps to the continuous noise level and vice versa, are defined in the real domain.The Approximating the diffusion process and the reverse process can be done with the sequence of noise levels $1>r_{1}>r_{2}> \cdots > r_{S} > 0$, instead of the variance schedule $\beta_{1}, \beta_{2}, \cdots, \beta_{T}$ of the original diffusion model where $S\ll T$ is the number of steps smaller than the original step $T$. Detailed derivation of the approximated diffusion process (VAR, STEPS) and the reverse process (DDPM-rev, DDIM-rev) is referred to the original paper.

Demonstrate performance of the proposed method in image and audio generation

The performance of the proposed method with respect to the number of steps $S$ is evaluated with pretrained image generation models of DDPM for CIFAR-10 / LSUN-bedroom and DDIM for CelebA, where $T=1000$.

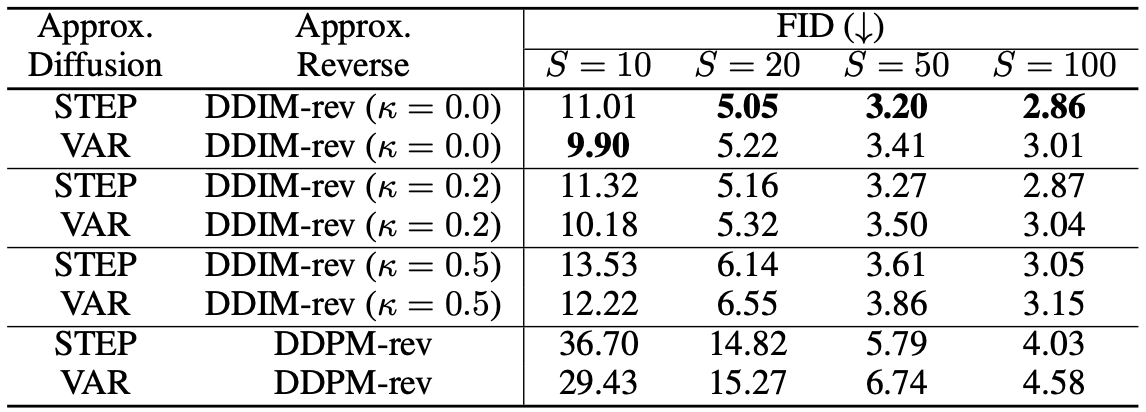CIFAR-10 image generation result (standard DDPM FID=3.03)

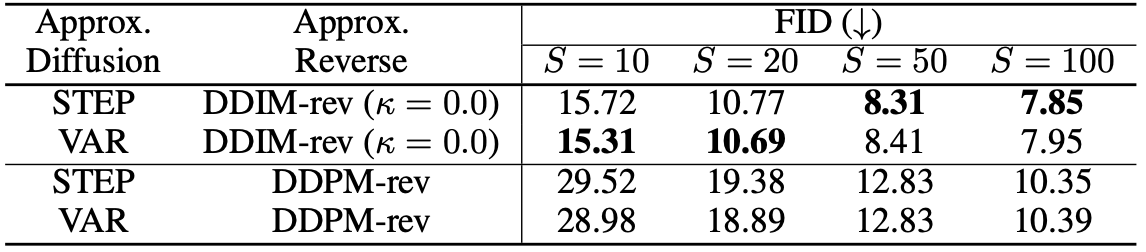CelebA image generation result (standard DDPM FID=7.00)

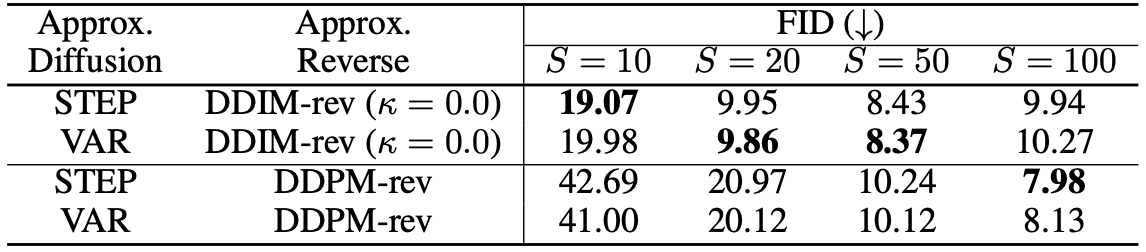LSUN-bedroom image generation result

The quantitative evaluation of image generation indicate that the FastDPM methods with shorter steps can generate images of comparable quality to that of the baselines. Also, DDIM-rev generally produces better quality images when compared to DDPM-rev.

For audio generation, pretrained DiffWave model for SC09 and LJSpeech is used where $T=200$.

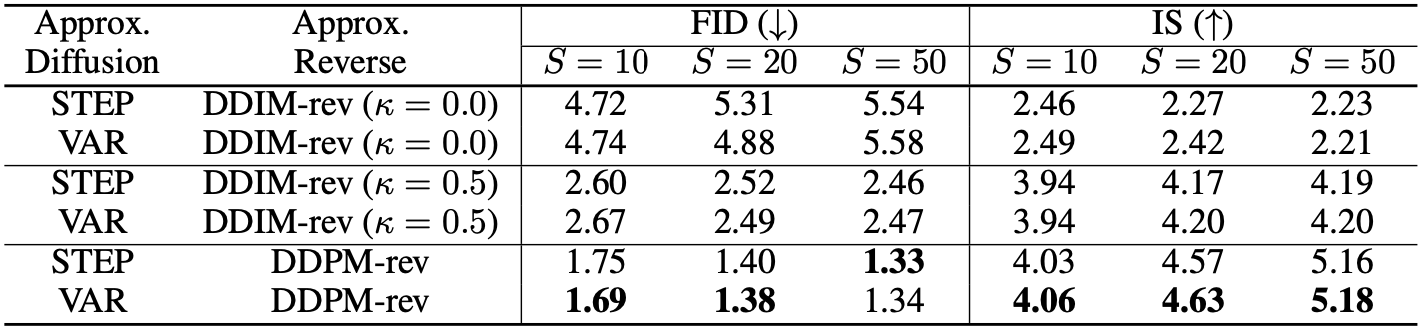SC09 unconditional audio generation result (standard DiffWave FID=1.29, IS=5.30)

LJSpeech audio generation conditioned on mel spectrogram MOS result

For audio generation, DDPM-rev generally produces better quality audio when compared to DDIM-rev. Another point that can be seen from the data synthesis experiments is that the variance schedule (VAR) tend to perform better for smaller number of steps $S$.

• Collaborative Score Distillation for Consistent Visual Synthesis
• Tackling the Generative Learning Trilemma with Denoising Diffusion GANs
• Palette: Image-to-Image Diffusion Models
• Image Synthesis and Editing with Stochastic Differential Equations
• Cascaded Diffusion Models for High Fidelity Image Generation