Significance
Keypoints
- Demonstrate restrictive Gaussian assumption of diffusion models
- Propose a method combining GANs with denoising diffusion process for faster sampling of high quality images with diversity
- Demonstrate performance of the proposed model by experiments
Review
Background
Recent progress in denoising diffusion models proved its ability to generate higher quality samples with more diversity when compared to generative adversarial networks (GANs). However, the diffusion models require a large number of sampling steps, restricting its usability in real-world tasks. The variational autoencoders (VAEs) and the normalizing flows are fast and are able to generate diverse samples, but quality of the generated image does not match that of the images generated from GANs or diffusion models. These three representative generative models cover up different two of the three problems, i.e. quality/speed/diversity, making up the problem which the authors call ‘The Generative Learning Trilemma’.
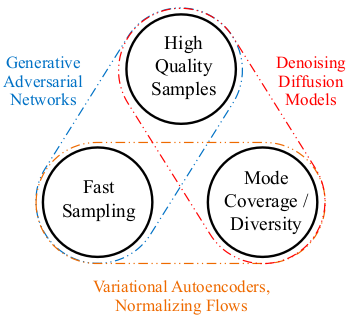The Generative Learning Trilemma
The trilemma is tackled first by theoretically understanding a restrictive assumption of diffusion models which causes the slowness, and this restriction is overcome by introducing GANs to model the denoising diffusion process.
Keypoints
Demonstrate restrictive Gaussian assumption of diffusion models
The diffusion process is modeled by a forward (adding noise) process and a reverse (removing noise; denoising) process. The forward process can be defined as:
\begin{equation} q(\mathbf{x}_{1:T}|\mathbf{x}_{0}) = \Phi_{t \geq 1} q(\mathbf{x}_{t} | \mathbf{x}_{t-1}), \quad q(\mathbf{x}_{t} | \mathbf{x}_{t-1}) = \mathcal{N} (\mathbf{x}_{t}; \sqrt{1-\beta_{t}} \mathbf{x}_{t-1},\beta_{t} \mathbf{I}), \end{equation}
where $q(\mathbf{x}_{0})$ is the real data distribution, $T$ is the number of steps for adding noise according to the pre-defined variance schedule $\beta_{t}$.
The reverse process is defined by:
\begin{equation} p_{theta}(\mathbf{x}_{0:T}) = p(\mathbf{x}_{T}) \Phi_{t \geq 1} p _{\theta} (\mathbf{x}_{t-1} | \mathbf{x}_{t}), \quad p_{\theta}(\mathbf{x}_{t-1} | \mathbf{x}_{t}) = \mathcal{N}(\mathbf{x}_{t-1};\mathbf{mu}_{\theta}(\mathbf{x}_{t},t), \sigma^{2}_{t}\mathbf{I}), \end{equation}
where $\mathbf{\mu}_{\theta}(\mathbf{x}_{t},t)$ and $\sigma^{2}_{t}$ are the mean and variance for the denoising model with learnable parameters $\theta$. The goal of the training is to optimize $\theta$ such that the divergence between the two distributions $q(\mathbf{x}_{t-1}|\mathbf{x}_{t})$ and $p_{\theta}(\mathbf{x}_{t-1}|\mathbf{x}_{t})$ are minimized.
However, the authors point out that two restrictive assumptions of the diffusion models are (i) denoising distribution $p_{\theta}(\mathbf{x}_{t-1}|\mathbf{x}_{t})$ is modeled with a Gaussian, and (ii) the number of denoising steps $T$ being large (order of thousands of steps).
Theoretically, the Gaussian assumption can be met in the limit of infinitesimal step size $\beta_{t}$ and the data marginal $q(\mathbf{x}_{t})$ being Gaussian. Faster sampling requires larger step size $\beta_{t}$ with smaller $T$, which violates the assumption leading to unsuccessful model performance.
Propose a method combining GANs with denoising diffusion process for faster sampling of high quality images with diversity
The authors mitigate the above mentioned restriction arising from Gaussian assumption by directly modeling complex conditional distributions with conditional GANs (which are capable of modeling them). Accordingly, the training objective is formulated as an adversarial loss: \begin{equation} \min_{\theta} \sum_{t \geq 1} \mathbb{E}_{q(t)} [D_{\mathrm{adv}}(q(\mathbf{x}_{t-1}|\mathbf{x}_{t})||p_{\theta}(\mathbf{x}_{t-1}|\mathbf{x}_{t}))]. \end{equation}
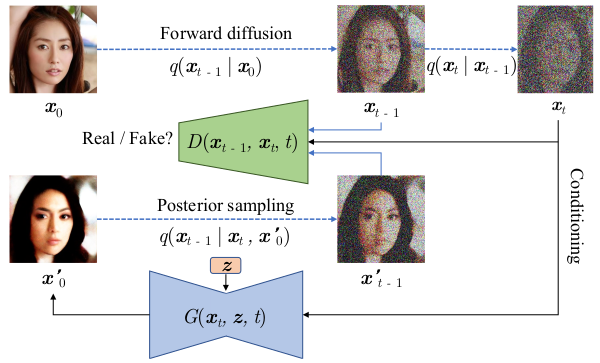Training process of the proposed denoising diffusion GAN
It can be seen that the denoising process is further conditioned on a random latent $\mathbf{z}$ further ensuring diversity of the generated samples. Advantage over one-shot GAN generator is that the denoising diffusion process introduces diversity to the generated images by mitigating mode collapse related to direct modeling of very complex real-data distribution.
Demonstrate performance of the proposed model by experiments
Quantitative results of image generation on CIFAR-10 show that the propsed method is better (higher IS and lower FID), faster (less time), and more diverse (higher recall score).
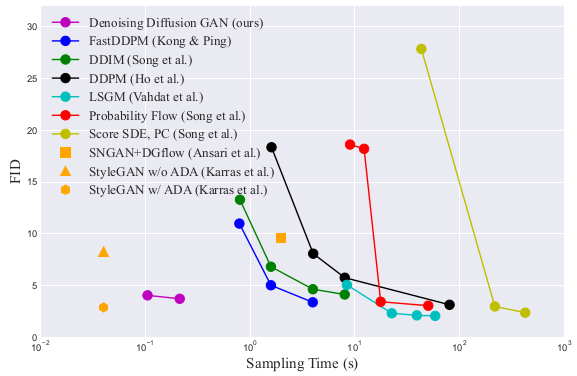Quality vs speed. StyleGANs take the bottom left position, but has less diversity (lower recall score)
Quantitative performance of the proposed method
Qualitative results also demonstrate the strength of the proposed method.
Qualitative results on CIFAR-10 dataset
Further results on other image datasets and ablation studies are referred to the original paper.
Related
- A Picture is Worth a Thousand Words: Principled Recaptioning Improves Image Generation
- Collaborative Score Distillation for Consistent Visual Synthesis
- Palette: Image-to-Image Diffusion Models
- Image Synthesis and Editing with Stochastic Differential Equations
- RewriteNet: Realistic Scene Text Image Generation via Editing Text in Real-world Image