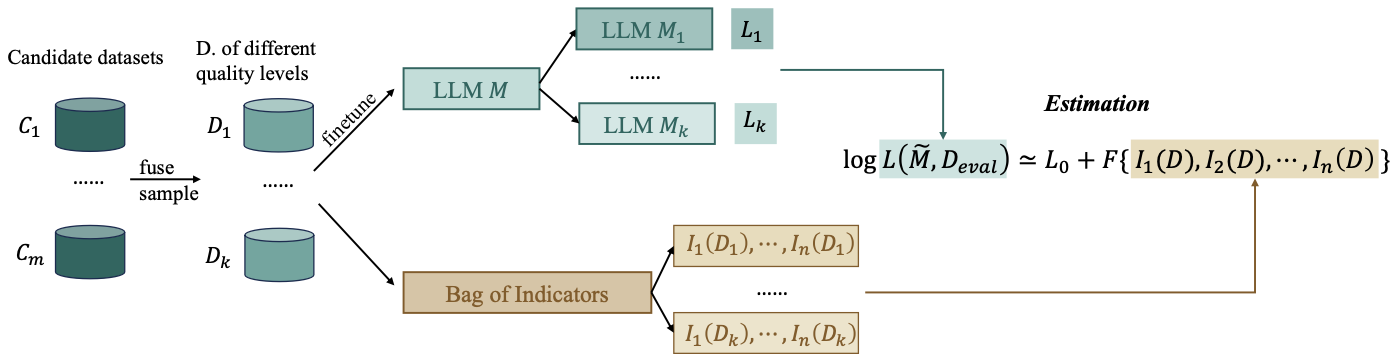
Significance
Keypoints
- Propose a method for training diffusion model that can conserve consistency across samples
- Demonstrate performance of the proposed method for panorama image editing, video editing, and 3d scene editing
Review
Background
While multi-modal image generation and editing has been successful with the latent diffusion models, such as the Stable Diffusion, its extension to video, 3D scene, or panorama (i.e. large) images has been less straightforward. Instead of changing the model architecture to extend its application, the authors bring their intuition that that many complex visual data are represented as a set of images constrained by modality-specific consistency. To this end, they leverage the power of pre-trained 2D latent diffusion models and add consistency across samples, which can be extended to various other visual tasks.
Keypoints
Propose a method for training diffusion model that can conserve consistency across samples
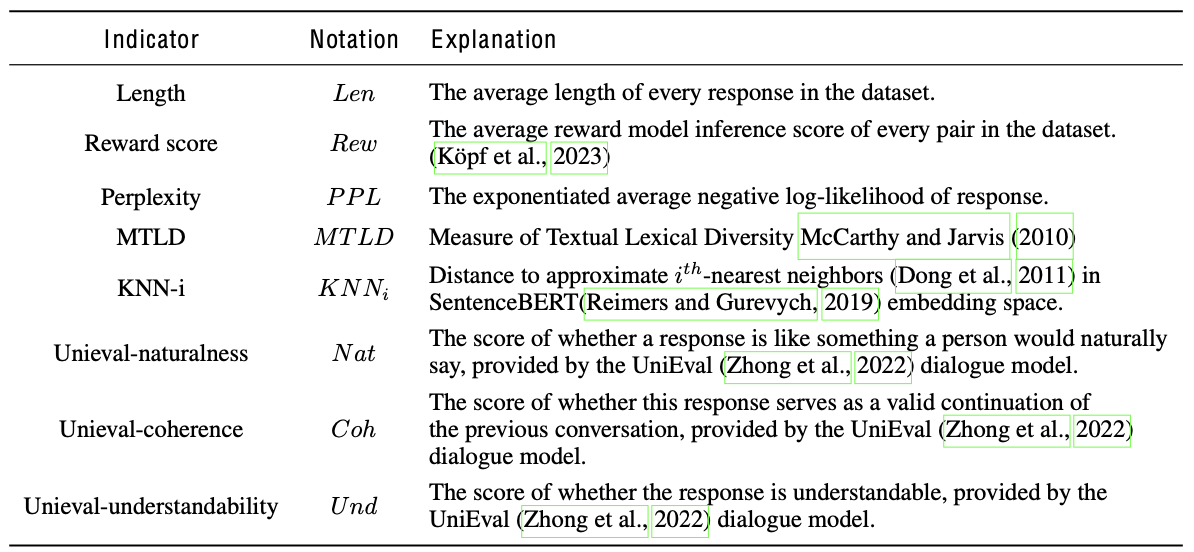
The proposed method starts from the Score Distillation Sampling (SDS), which allows optimization of any differentiable function $g$ on the image domain: \begin{equation}\label{eq:sds} \mathcal{L} _{Distill} (\theta ; \mathbf{x} = g(\theta )) = \mathbb{E}_{t, \epsilon} [ \alpha _{t} / \sigma _{t} D _{KL} (q (\mathbf{x} | \mathbf{x} = g(\theta )) || p^{\omega}_{\theta} (\mathbf{x}_{t} ; y , t))], \end{equation} where $\mathbf{x}$ is the image, $\theta$ is the parameter of $g$, $y$ is the text prompt condition, and $t$ is the timestep of the diffusion process. The equation can be re-formulated for the practical implementation as \begin{equation}\label{eq:sdsimpl} \nabla _{\theta} \mathcal{L}_{SDS} (\theta ; \mathbf{x} = g(\theta)) = \mathbb{E}_{t,\epsilon} [ w(t) (\mathbf{\epsilon}^{\omega}_{\theta} (\mathbf{x}_{t}; y, t ) - \mathbf{\epsilon} ) \frac{\partial \mathbf{x}}{\partial \theta} ], \end{equation} where $t ~ \mathcal{U}(t_{min}, t_{max})$ and $\mathbf{\epsilon} ~ \mathcal{N}(\mathbf{0}, \mathbf{I})$
Now, the authors aim to solve the Eq. \eqref{eq:sds} with Stein variational gradient descent (SVGD; Please refer to the original work for details) and update a set of $N$ parameters ${\theta_{i} }^{N}_{i=1}$ that handles images $\mathbf{x}^{(i)} = g(\theta _{i})$: \begin{equation}\label{eq:csd} \nabla _{\theta_{i}} \mathcal{L}_{CSD} (\theta_{i} ) = \frac{w(t)}{N} \sum^{N}_{j=1}( k(\mathbf{x}^{(j)}_{t}, \mathbf{x}^{(i)}_{t}) (\mathbf{\epsilon}^{w}_{\phi} (\mathbf{x}^{(j)}_{t} ; y, t ) - \mathbf{\epsilon} ) + \nabla _{\mathbf{x}_{t}^{(j)}} k(\mathbf{x}^{(j)}_{t}, \mathbf{x}^{(i)}_{t}) ) \frac{\partial \mathbf{x}^{(i)}}{\partial \theta _{i}} , \end{equation} where $k$ is a kernel function, such as a Radial Basis Function (RBF), and CSD stands for the “Collaborative Score Distillation”. Now, this is equivalent to the Eq. \eqref{eq:sdsimpl} when $N=1$, generalizing it to encourage similar samples to exchange more score updates, and discourage different samples to interchange score information less. The CSD can be extended for the text-guided editing (CSD-Edit) which the details of derivation is referred to the original work.
 Schematic illustration of the proposed CSD
Schematic illustration of the proposed CSD
Demonstrate performance of the proposed method for panorama image editing, video editing, and 3D scene editing
The authors provide qualitative and quantitative results for i) panorama image editing, ii) video editing, and iii) 3D scene editing.
Qualitative results
The qualitative results suggests excellent performance for text-guided editing of panorama image, video, and 3D scene.
 Qualitative results of CSD-Edit for text-guided panorama image editing
Qualitative results of CSD-Edit for text-guided panorama image editing
 Qualitative results of CSD-Edit for text-guided video editing
Qualitative results of CSD-Edit for text-guided video editing
 Qualitative results of CSD-Edit for text-guided 3D scene editing
Qualitative results of CSD-Edit for text-guided 3D scene editing
Quantitative results
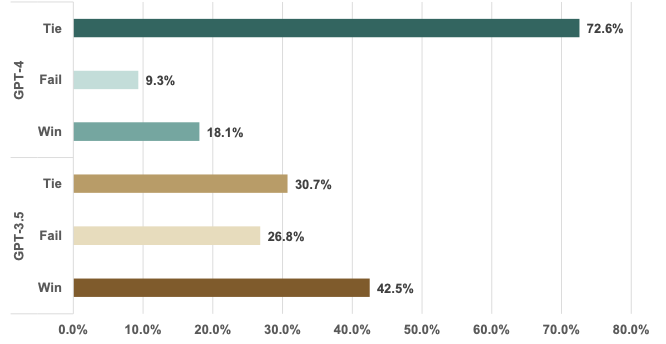
Quantatitve results also suggest superiority of the proposed method over other previous baselines.
 Quantitative results of CSD-Edit for text-guided editing of panorama image, video, and 3D scene
Quantitative results of CSD-Edit for text-guided editing of panorama image, video, and 3D scene
Further results can be found at the authors’ project page.