Significance
Keypoints
- Propose a method that can evaluate the quality of instruction-tuning purpose dataset
- Demonstrate feasibility of the proposed method by experiments
Review
Background
Instruction tuning is an important technique for fine-tuning large language models to achieve better performance on specific instructions. The data for performing instruction tuning is based on natural language which includes pairs of instructions and corresponding responses, making it not straightforward to evaluate the quality of the datasets. The authors propose InstructMining to quantify the quality of the instruction-following data and show that better results can be expected when language models are trained with high quality dataset selected with InstructMining.
Keypoints
Propose a method that can evaluate the quality of instruction-tuning purpose dataset
The main assumption of the proposed method is that quality $Q$ of the instruction-following dataset $D$ can be estimated through the inference loss $L$ of a LM $\tilde{M}$ instruction-tuned with $D$ on a separate high-quality evaluation dataset $D_{eval}$.
\begin{equation}\label{eq:1} Q _{D|M,S}\propto -L ( \tilde{M}, D_{eval}), \end{equation} where $M$ is the LM before the instruction tuning.
However, it is often often ineffeicient to fine-tune a large LM to evaluate the dataset quality. Accordingly, the authors propose to fit a multivariate linear model from a set of conventional indicators $I = {I_{i}, i \in N }$ to estimate the $-L( \tilde{M}, D_{eval})$ of Eq. \eqref{eq:1}:
\[-Q \_{D|M,S}\propto \log L ( \tilde{M}, D\_{eval}) \propto L\_{0} + F (\{ I\_{1}(D), I\_{2}(D), ..., I\_{n}(D) \} ),\]where $F$ is the linear multivariate weighted sum.
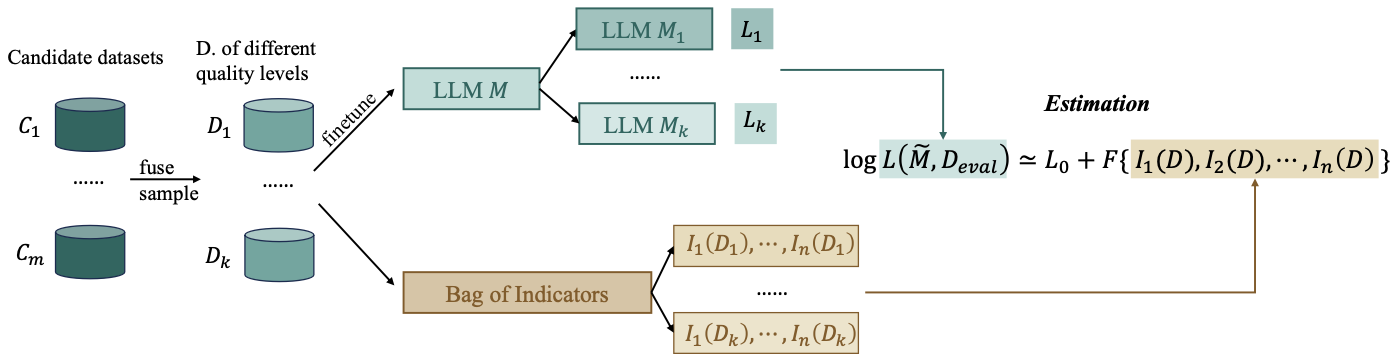Schematic illustration of the proposed method
The list of conventional indicators $I$ is provided on the following table.
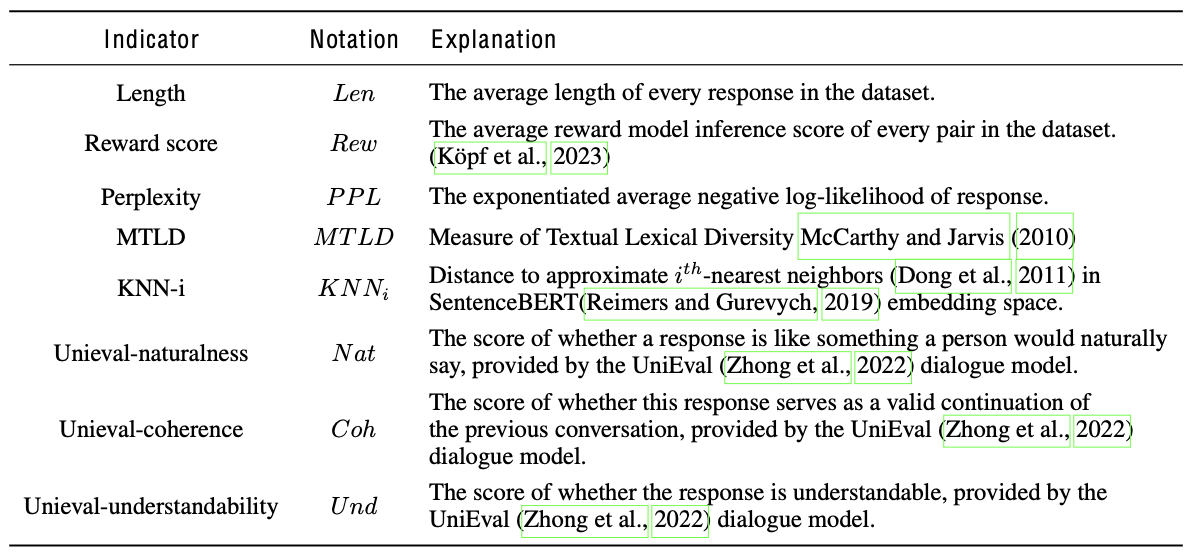Conventional natural language indicators
The authors fit the multivariate regression model with least squares estimation and obtain following equation for practical quantification of the dataset quality:
\[\log L ( \tilde{M}, D\_{eval}) \propto 1.0694 - 0.1498 Rew + 8.257 * 10^{-5} Len - 0.9350 Knn\_{6} + \epsilon,\]where $\epsilon$ represents the random error.
Demonstrate feasibility of the proposed method by improved instruction-tuned result
Feasibility of the proposed method is demonstrated by selecting high-quality instruction-following dataset based on the proposed method.
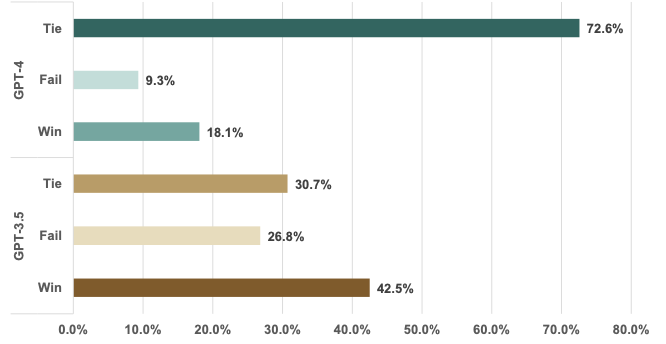GPT evaluation comparison between the InstructMining selected dataset and randomly sampled dataset
It can be seen that the GPT3.5 model fine-tuned with InstructionMining selected dataset perform better on the direct comparison. Other experiments include univariate analysis of indicators, and evaluating the loss and loss difference per experiments, which can be found in the original work.