Significance
Keypoints
- Explore architecture of diffusion models and add classifier guidance for improving image generation
- Demonstrate quality of the generated image by experiments
Review
Background
Diffusion model is a parameterized Markov chain that gradually converts one distribution to another, first proposed in the paper Deep Unsupervised Learning using Nonequilibrium Thermodynamics. Recent improvement in diffusion models like Denoising Diffusion Probabilistic Models (DDPM) has shown promising results in image generation, which is comparable to the state-of-the-art GAN models. Although adversarial models can generate high quality images, some common limitations of GAN include lack of diversity of generated images (mode collapse) or difficulty in training. The authors claim that the diffusion model, which is less prone to the above limitations of GANs, could not generate images better than GAN not because of the approach itself, but because of little exploration on architectural and training details. Surprisingly, this claim is supported by the experiments. Can diffusion models be the next standard option for image generation?
Keypoints
Explore architecture of diffusion models and add classifier guidance for improving image generation
The DDPM aims to gradually denoise a full noise $x_{T}$ to a clean image $x_{0}$ within timestep $t \in {1,…,T}$.
Thus, the noisy image at timestep $t$ is $x_{t}$ a mixture of noise $\epsilon$ and signal $x_{0}$ where the level of noise is dependent on $t$.
A diffusion model $\epsilon_{\theta}(x_{t},t)$ aims to extract the noise component from $x_{t}$, so the training objective is simply a mean-squared error between the true noise and the model-predicted noise:
\begin{equation}
||\epsilon_{\theta}(x_{t},t)-\epsilon||^{2}.
\end{equation}
The key point of DDPM is that under certain assumptions, the distribution $p_{\theta}(x_{t-1}|x_{t})$ can be modelled as a diagonal Gaussian $\mathcal{N}(x_{t-1};\mu_{\theta}(x_{t},t),\sigma_{\theta}(x_{t},t))$ where the mean $\mu_{\theta}$ can be calculated as a function of the diffusion model $\epsilon_{theta}$, and variance $\sigma_{\theta}$ can be fixed to a constant.
Now that $p_{\theta}(x_{t-1}|x_{t})$ is modelled, the clean image $x_{0}$ can be obtained from a Gaussian noise $x_{T}$ by $p_{\theta}(x_{0}:T):=p(x_{T})\Pi ^{T}_{t=1}p_{\theta}(x_{t-1}|x_{t})$.
The Denoising Diffusion Implicit Model (DDIM) tries to formulate DDPM with an alternative non-Markovian noising process to reduce the number of timesteps $T$ required for sampling.
Schematic illustration of the DDPM (left) and the DDIM (right)
Explore architecture of diffusion models
The diffusion models usually inherit the UNet architecture, with some modifications such as global attention at 16$\times$16 resolution, or timestamp embedding projection.
The authors explore optimal architecture of the diffusion models by comparative/ablative studies.
Points of the exploration are: (i) depth vs width (ii) number of attention heads (iii) using attention at different resolutions (iv) using BigGAN residual block for up/downsampling (v) rescaling residual connections (vi) using AdaGN.
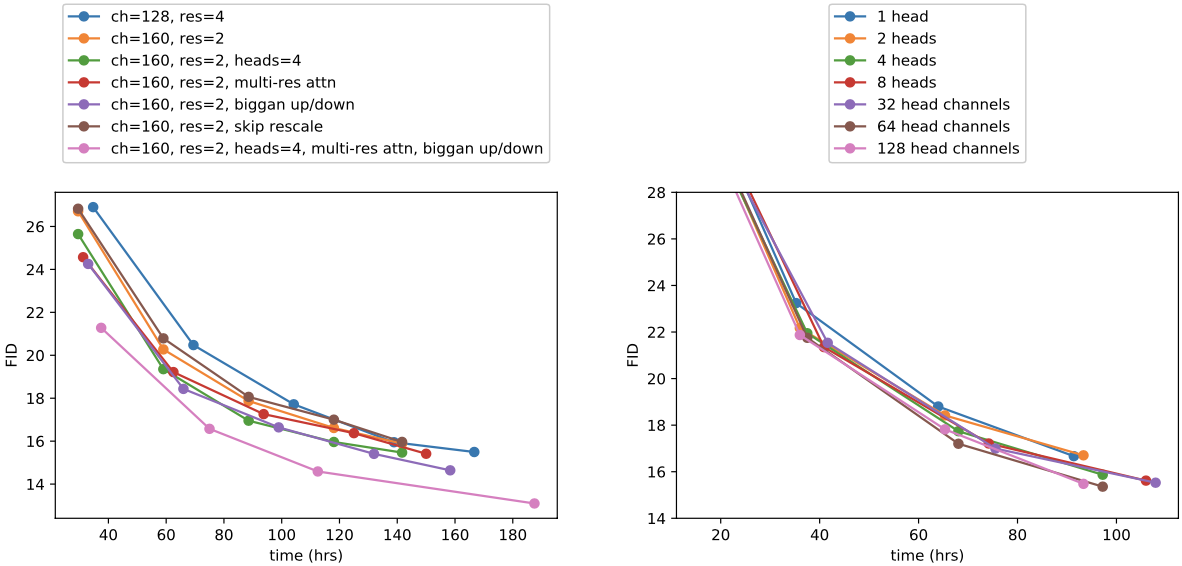Model architecture exploration results
Based on the above result, the authors use multiple-heads with 64 channels per head, 2 residual blocks, multi-resolution attention at 32, 16, 8 resolutions, BigGAN up/downsampling, and AdaGN layer for the rest of the experiments.
Add classifier guidance
Generative models usually can benefit from exploiting a image-label classifier $p(y|x)$.
The authors propose to train a classifier $p_{\phi}(y|x_{t},t)$ on noisy images $x_{t}$ and use gradients $\nabla_{x_{t}}\log p_{\phi}(y|x_{t},t)$ to guide the diffusion sampling process towards the class label $y$.
Classifier guidance for diffusion models
It was empirically found that scaling the gradient with $s>1$ result in producing a more realistic image, but with less diversity.
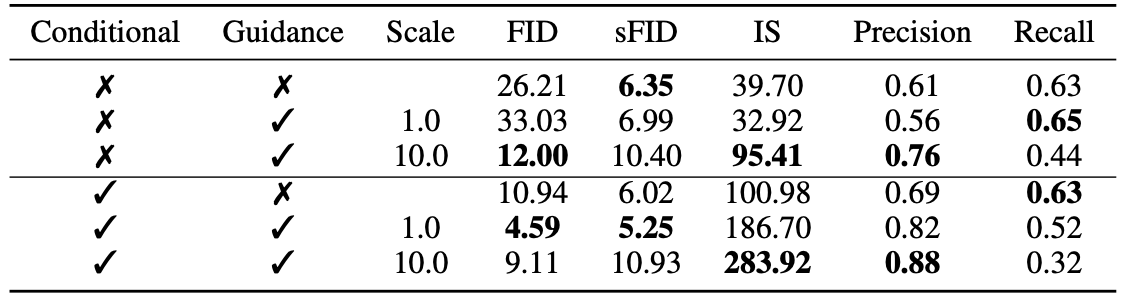Effect of classifier guidance and gradient scaling in sample quality
The mathematical derivation of the classifier guidance is referred to the original paper.
Demonstrate quality of the generated image by experiments
The proposed model with classifier guidance is referred to as Ablated Diffusion Model with Guidance (ADM-G).
The sample quality and diversity is evaluated by the FID as the main metric.
To further evaluate fidelity, precision or Inception Score (IS) are used while recall is used to further evaluate diversity.
The ADM-G outperforms the GAN based SOTA conditional model BiGGAN and SOTA unconditional model StyleGAN2 with various datasets including the LSUN and the ImageNet.
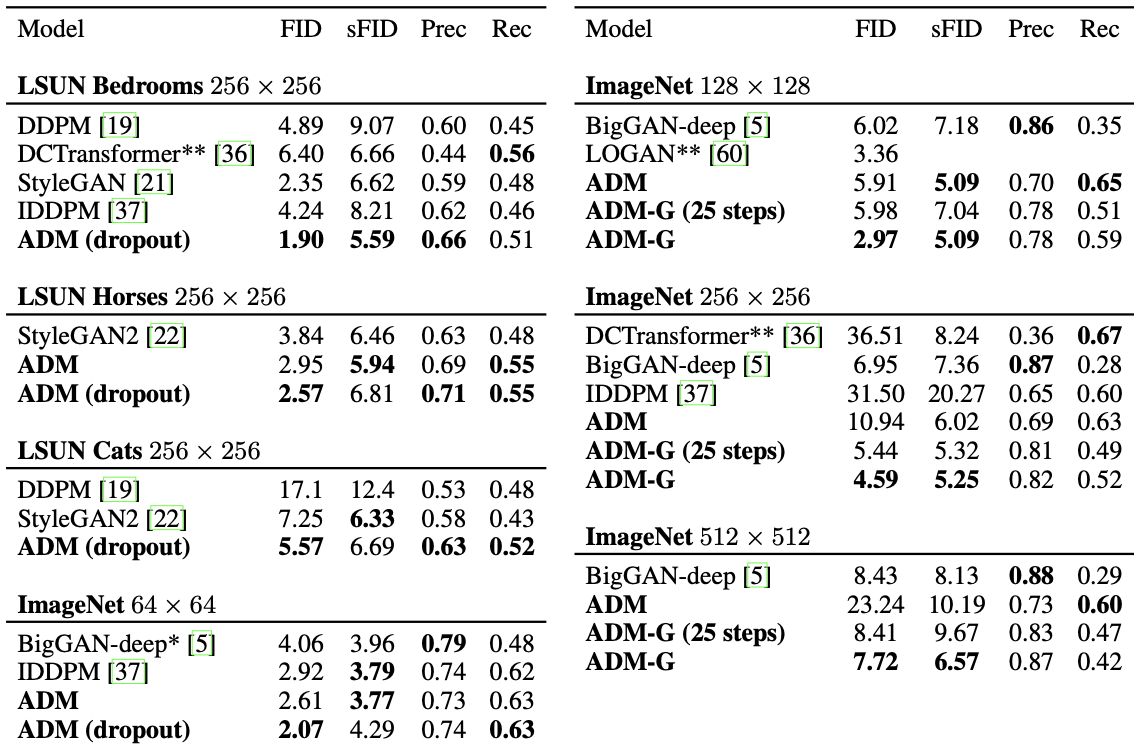Quantitative result of the proposed method
Qualitative result compared with BigGAN (left), proposed (middle), and training samples (right)
As the title of this paper indicates, significance of this paper can be summarized in one sentence:
Diffusion models beat GANs on image synthesis!
Other qualitative results and theoretical/practical details are referred to the original paper.
Related
- A Picture is Worth a Thousand Words: Principled Recaptioning Improves Image Generation
- Collaborative Score Distillation for Consistent Visual Synthesis
- Tackling the Generative Learning Trilemma with Denoising Diffusion GANs
- Palette: Image-to-Image Diffusion Models
- Image Synthesis and Editing with Stochastic Differential Equations