Significance
Keypoints
- Demonstrate implicit loss of negative sampling inducing sampling bias
- Show that the implicit loss can help learning on long-tail data distribution
Review
Background
For training a model for a multi-class classification task, surrogate loss $l:\mathcal{Y}\times \mathbb{R}^{L}\rightarrow \mathbb{R}_{+}$ such as the cross-entropy loss: \begin{equation}\label{eq:xent} l(y, f(x)) = -f_{y}(x) + \log [\sum_{y^{\prime} \in [L]} e^{f_{y^{\prime}(x)}}] = \log [ 1+ \sum_{y^{\prime}\neq y} e^{f_{y^{\prime}}(x)-f_{y}(x)}]. \end{equation} or the decoupled loss (e.g. hinge loss): \begin{equation}\label{eq:decoupled} l(y,f(x)) = \phi (f_{y}(x)) + \sum_{y^{\prime}\neq y}\varphi(-f_{y^{\prime}(x)}), \end{equation} are where $x$ is the input, $y\in \mathcal{Y} = [L]={1,2,…,L}$ is the label, $f$ is the model, $\phi,\varphi: \mathbb{R}\rightarrow\mathbb{R}_{+}$ are margin losses. The problem becomes more difficult as the number of label classes increase. This difficulty comes not only from inherent limitation of the surrogate loss functions for learning multi-class decision boundary, but also from practical limitation that classes with rare labels are more common for multi-class datasets. To deal with rare labels, negative sampling methods that draw samples from a distribution $q$ representing the negative examples or weighting the loss with suitable weight $w$ are widely used. Some of the popular choices for the sampling distribution $q$ are (i) model-based, (ii) uniform, and (iii) within-batch, while choices for the weighting scheme $w$ include (i) importance weighting, (ii) constant, and (iii) relative weighting. Another line of negative sampling methods.
Keypoints
Demonstrate implicit loss of negative sampling inducing sampling bias
The sampling distribution $q$ and the weighting scheme $w$ can be incorporated into the losses \eqref{eq:xent} and \eqref{eq:decoupled} as:
\begin{equation}
l(y,f(x); \mathcal{N},w) = \log [1+\sum_{y^{\prime}\in \mathcal{N}}w_{yy^{\prime}}\cdot e^{f_{y^{\prime}}(x)-f_{y}(x)}],
\end{equation}
and
\begin{equation}
l(y, f(x); \mathcal{N},w) = \phi(f_{y}(x))+ \sum\nolimits_{y^{\prime}\in \mathcal{N}} w_{yy^{\prime}}\cdot \varphi (-f_{y^{\prime}}(x)),
\end{equation}
where $\mathcal{N}$ is the set of negative samples from the distribution $q$.
The authors derive the implicit loss being optimized for widely used options of $q$ and $w$.
Implicit loss for choices of sampling distribution $q$ and weighting scheme $w$
It is noted that the uniform and within-batch methods with constant weights (which is a predominant method in practice) induce sampling bias, where the negative labels receive a variable penalty.
Detailed derivation process is referred to the original paper.
Show that the implicit loss can help learning on long-tail data distribution
The sampling bias suggest that popular negative sampling schemes do not faithfully approximate the original loss.
However, the authors also observe that the implicit loss of the sampled softmax cross-entropy loss is similar to a the softmax with pairwise label margin:
\begin{equation}\label{eq:margin}
l^{\rho}_{\text{mar}}(y, f(x)) = \log [1+\sum_{y^{\prime}\neq y}\rho_{yy^{\prime}} \cdot e^{f_{y^{\prime}}(x)-f_{y}(x)}],
\end{equation}
where $\rho_{yy^{\prime}}$ is the desired margin between $y$ and $y^{\prime}$.
The loss \eqref{eq:margin} is used for long-tail learning since it allows for greater emphasis on prediction of rare classes.
The authors derive that the negative sampling scheme can thus work as a suitable loss for long-tail learning.
Experiments on long-tail CIFAR-100 and ImageNet datasets indicate that within-batch sampling with constant weighting helps on the tail.
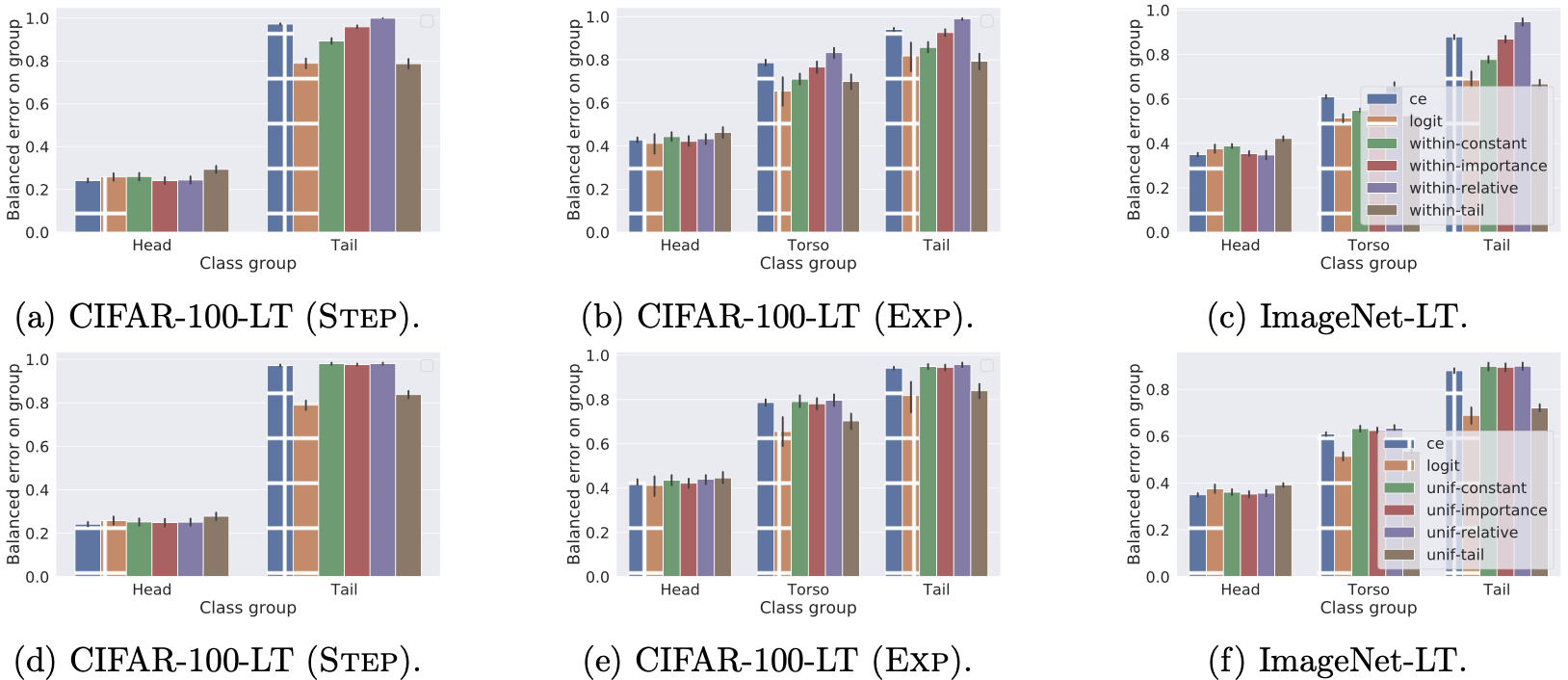Long-tail image classification results on various sampling/weighting schemes
Results on retrieval benchmarks AmazonCat-13k and WikiLSHTC-325k also support the notion that the within-batch sampling with constant weighting helps on the tail.
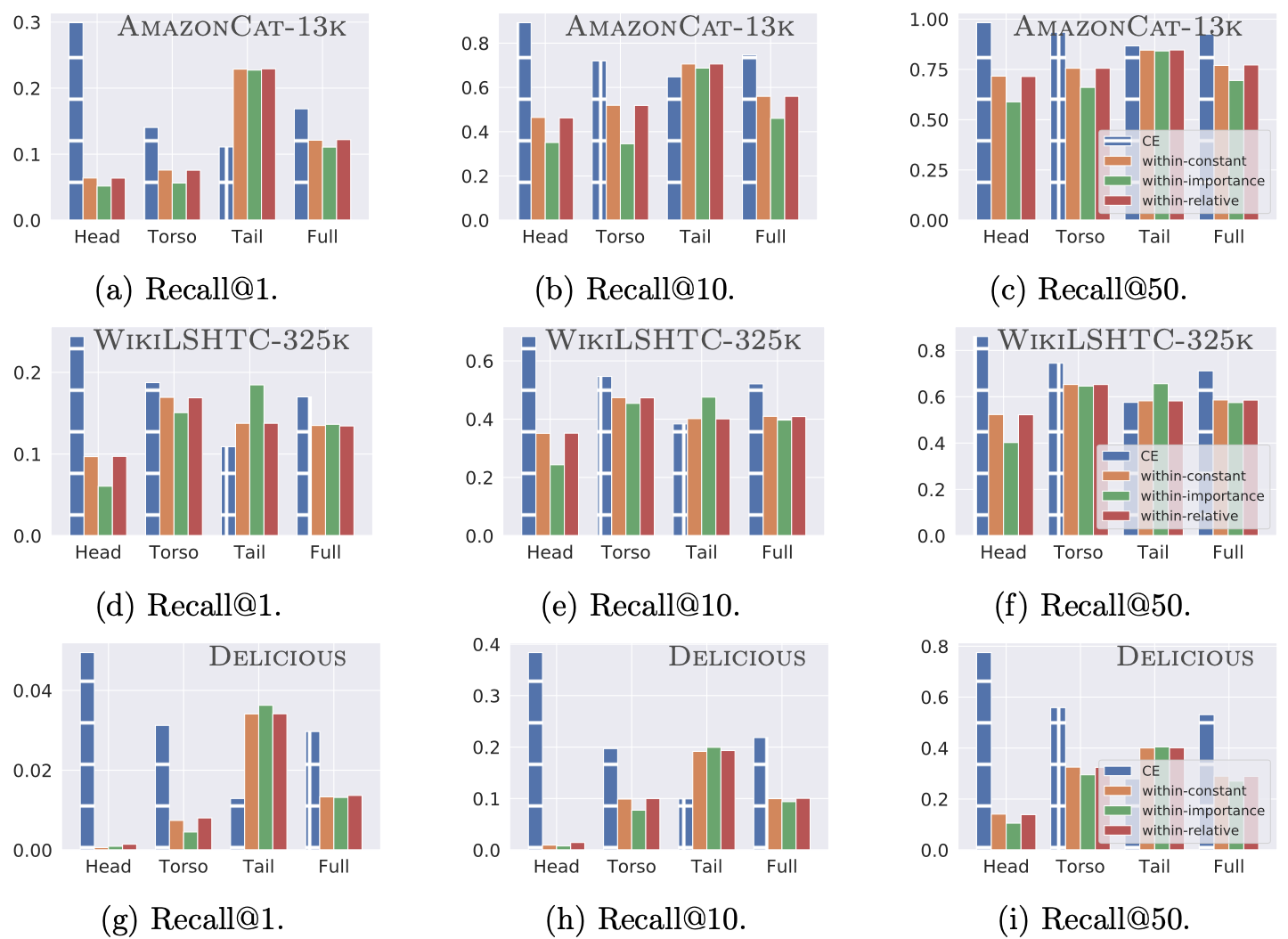Experimental result on retrieval benchmarks with large number of classes