[2111.01004] Improving Contrastive Learning on Imbalanced Seed Data via Open-World Sampling

• Propose an open-world data sampling strategy for contrastive learning
• Demonstrate effectiveness of the proposed method by experiments

Background

Self-supervised contrastive learning exploits unlabelled data to learn the representation of the input distribution. This may sound like that crawling large number of unlabelled images from open world source, such as the internet, can make deep neural networks better and better. Unfortunately, it is not the case in the real world setting. For example, initial data distribution may be skewed, Representation of classes with little number of samples, i.e. tail classes, may not be sufficiently learned, redundant samples may be repeatedly affect the model to be biased, and so on. The authors address this issue in open world sampling and propose a strategy for balanced data sampling.

Keypoints

Propose an open-world data sampling strategy for contrastive learning

The problems mentioned in the Background section includes what the authors denote tailness, proximity, and diversity.

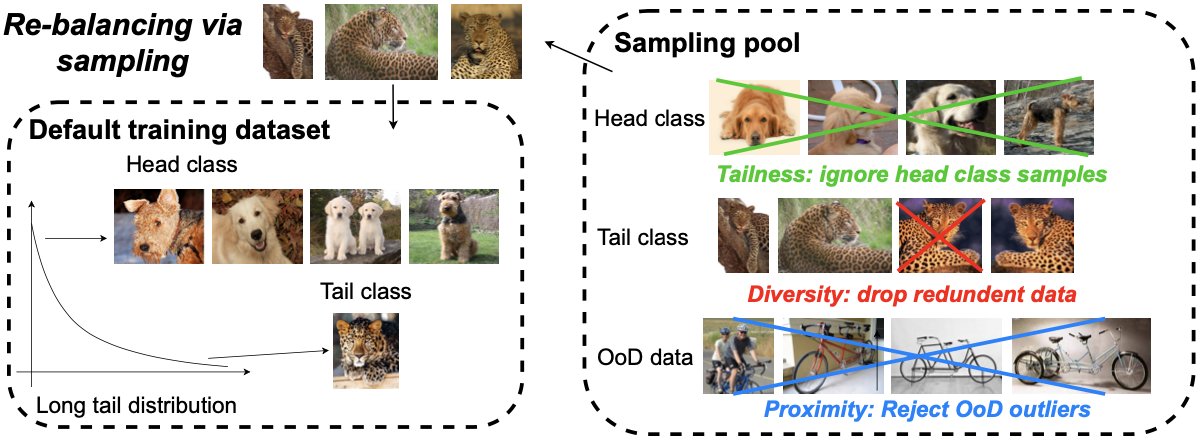Consideration for balanced open world sampling

Tailness refers to the need for sampling data from tail classes, i.e. minor classes with small number of samples. Encouraging sampling from tail class have been addressed in previous studies by selecting the samples with large supervised loss values. However, this practice can be suboptimal in contrastive learning setting because the loss for contrasting two augmentations maybe prone to occasional large loss values even if the sample is from the head class. The authors propose to smooth out the random augmentation contrastive loss by taking expectation (i.e. average) of the loss from the samples as follows: \begin{equation} \label{eq:ecle} \mathcal{L}^{\mathcal{E}}_{\text{CL},i} = \mathbb{E}_{\theta_{i,1}, \theta_{i,2} ~ \Theta} (\mathcal{L}_{\text{CL},i} (\theta_{i,1},\theta{i,2};\tau , v_{i}, V^{-})). \end{equation} This loss is referred to as the empirical contrastive loss expectation (ECLE) for the $i$-th sample.

Although ECLE can encourage sampling of tail classes, it can also encourage unwanted samples (completely unseen/unwanted class sample, OOD outliers) to be chosen. The authors add a regularizing term to the ECLE that promotes proximity of samples via discouraging OOD samples by: \begin{equation} \label{eq:proximity} D(s^{0},s^{1}) = \frac{1}{|s^{1}|} \sum_{j \in s^{1}} \min_{i \in s^{0}} \Delta (x_{i}, x_{j}), \end{equation} where $s^{0}$ is the seed training set, $s^{1}$ is the newly sampled training set, $\Delta$ is the feature distance (normalized cosine distance in the paper) between the two samples, and $D$ is the average feature distance. Here, the authors precompute the set of feature prototypes of $s^{0}$ by using $K$-means clustering for efficiency.

A final consideration in open-world sampling for efficient contrastive learning is to reduce redundant samples by promoting diversity. The authors add another regularization term to the ECLE formulated as: \begin{equation} \label{eq:diversity} H(s^{1}\cup s^{0}, S_{all}) = \max_{i \in S_{all}} \min _{j \in s^{1} \cup s^{0}} \Delta (x_{i}, x_{j}), \end{equation} where $S_{all}$ denotes all samples from $s_{0}$ and $s_{1}$.

The final objective can be formulated as a constrained optimization including all \eqref{eq:ecle}, \eqref{eq:proximity}, \eqref{eq:diversity}: \begin{equation} \label{eq:mak} \max _{s^{1}:|s^{1}| \leq K} { \sum_{i \in s^{1}} \mathcal{L}^{\mathcal{E}}_{\text{CL}, i} - D(s^{0}, s^{1}) - H(s^{1} \cup s^{0, S_{all})}) }. \end{equation} The authors name this final objective \eqref{eq:mak} as Model-Aware K-center (MAK), and propose to solve this NP-hard problem by greedy algorithm.

Pseudocode for solving MAK optimization problem

Demonstrate effectiveness of the proposed method by experiments

The authors demonstrate the effectiveness of the proposed method in contrastive learning by comparing it with random sampling and vanilla K-center sampling for linear downstream finetuning and few-shot learning.

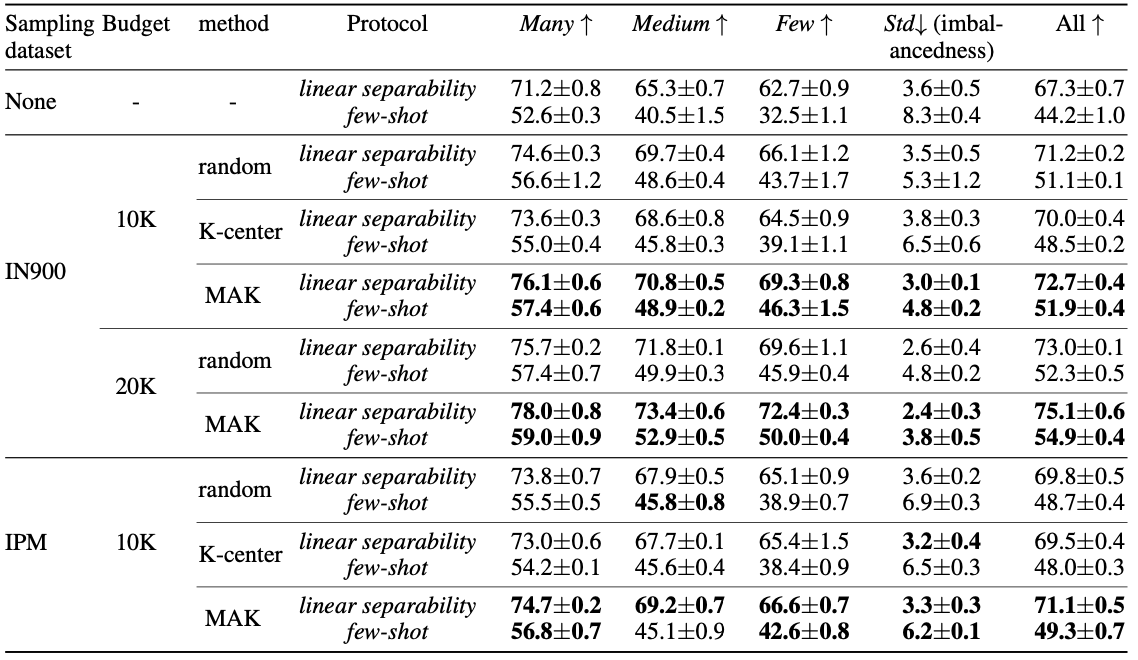Quantitative performance of the proposed method

It can be seen that the proposed method outperforms other baseline sampling methods in the most budget settings given the ImageNet-900 (IN-900) and ImageNet-Places-Mix (IPM) dataset.

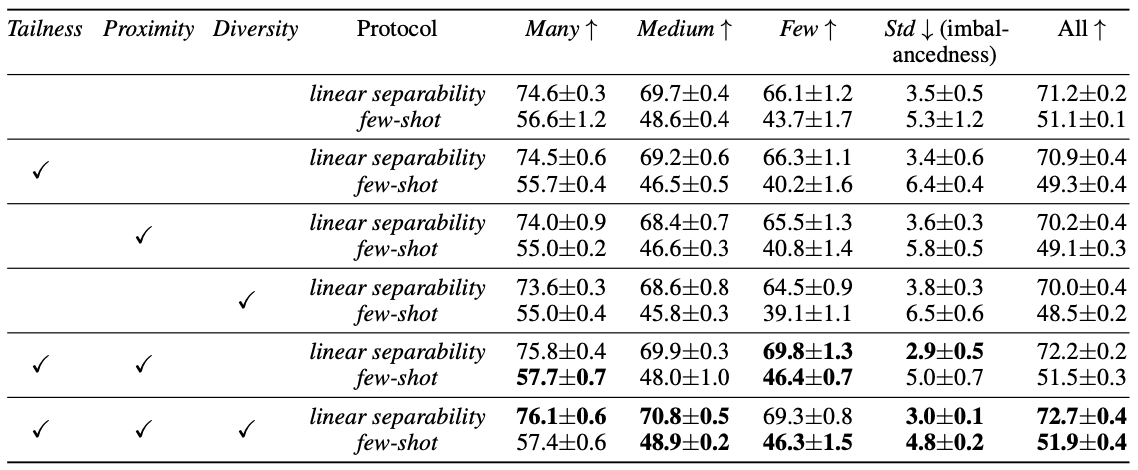Ablation study results Ablating each components of the MAK degrades its performance, suggesting importance of each proposed objectives in current experimental setting.

Further analyses include correlation of ECLE proxy with data distribution, computational overload analysis, imbalanced downstream task analysis, and diversity visualization which are referred to the original paper

• LiT: Zero-Shot Transfer with Locked-image Text Tuning
• On Model Calibration for Long-Tailed Object Detection and Instance Segmentation
• Disentangling Sampling and Labeling Bias for Learning in Large-Output Spaces