[2107.02170] On Model Calibration for Long-Tailed Object Detection and Instance Segmentation

• Propose a model-agnostic method for improving performance of models trained with long-tailed dataset
• Demonstrate performance gain with the proposed method on object detection and instance segmentation tasks

Background

Object detection and instance segmentation are key tasks in computer vision that can be applied to many fields. While training a neural network is a de facto solution for these tasks, class imbalance of the training dataset limits the final test performance of the models because confidence score of a rare class is generally low at test time. Although previous attempts have been made to address this issue at training phase (e.g. by sampling / weighting methods), the authors try to recalibrate the confidence score at test time. 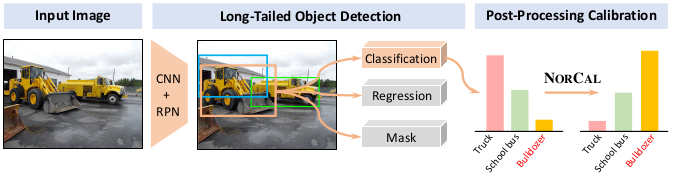Test-time approach for long-tailed object detection The main idea is simple: calibrating the confidence score with respect to the number of training samples in the training dataset per class while handling the background class separately.

Keypoints

Propose a model-agnostic method for improving performance of models trained with long-tailed dataset

Object detection and instance segmentation models are commonly trained with a cross entropy loss, \begin{align} \mathcal{L}_{\text{CE}}(\mathbf{x},\mathbf{y}) = -\sum^{C+1}_{c=1}y[c] \times \log (p(c\mid \mathbf{x})). \end{align} where $\mathbf{y} \in { 0,1 }^{C+1}$ is the one-hot ground truth label and $p(c\mid \mathbf{x})$ is the predicted confidence score of the proposal $\mathbf{x}$ belonging to the class $c$: \begin{align} p(c\mid \mathbf{x}) = \frac{\exp(\phi_{c}(\mathbf{x}))}{\sum^{C}_{c\prime =1}\exp(\phi_{c\prime}(\mathbf{x}))+\exp(\phi_{C+1}(\mathbf{x}))}. \end{align} Here, $\phi_{c}$ is the logit for class $c$.

To calibrate the confidence score with respect to number of training samples $N_{c}$ for class $c$: \begin{align} p(c\mid \mathbf{x}) = \frac{\exp(\phi_{c}(\mathbf{x})/a_{c})}{\sum^{C}_{c\prime =1}\exp(\phi_{c\prime}(\mathbf{x}))/a_{c\prime} + \exp(\phi_{C+1}(\mathbf{x}))}, \end{align} where $a_{c}$ monotonically increases with $N_{c}$. The authors further show that normalization of the scores by number of samples does not hurt the performance of the head (majority) class prediction.

Demonstrate performance gain with the proposed method on object detection and instance segmentation tasks

Performance gain of existing methods is consistently found by applying the proposed NorCal on the LVISv1 dataset. 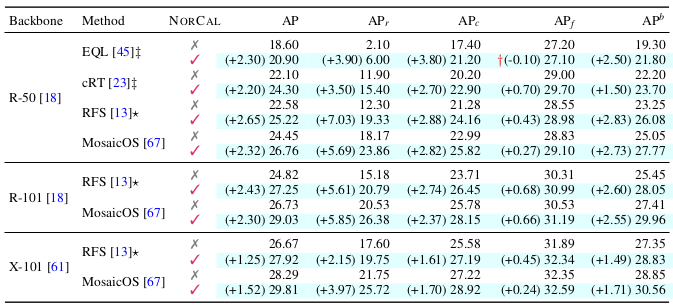Effect of applying NorCal to existing models on the LVISv1 dataset This improvement of performance is also significant when compared to other baseline post-calibration methods. 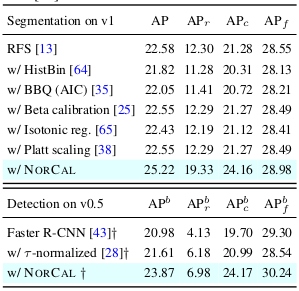Comparison to existing post-calibration methods

Qualitative result of the proposed method on object detection

Other ablation studies and model analysis results are referred to the original paper.

• Bootstrap Your Object Detector via Mixed Training
• Improving Contrastive Learning on Imbalanced Seed Data via Open-World Sampling
• SimROD: A Simple Adaptation Method for Robust Object Detection
• Per-Pixel Classification is Not All You Need for Semantic Segmentation
• Disentangling Sampling and Labeling Bias for Learning in Large-Output Spaces