Significance
Keypoints
- Apply invertible neural network to solve RAW to RGB image signal processing problem in an end-to-end manner
- Show qualitative and quantitative strengths over a few baseline models
Review
Background
The invertible neural network (INN) is a class of the generative models, along with the generative adversarial network (GAN) and the variational auto-encoder (VAE). Although INNs inherit solid theoretical background and its clever implementation, practical application for image generation task has been limited by its relative under-performance compared to the GANs or the VAEs. However, recent works are starting to recognize the potential strength of the INNs for solving image-processing problems, which can benefit from explicit invertibility. This work also exploits the invertibility of the INN to train an end-to-end model that can convert RAW image data to a compressed JPEG data, and vice versa.
Keypoints
Apply invertible neural network to solve RAW to RGB image signal processing problem in an end-to-end manner
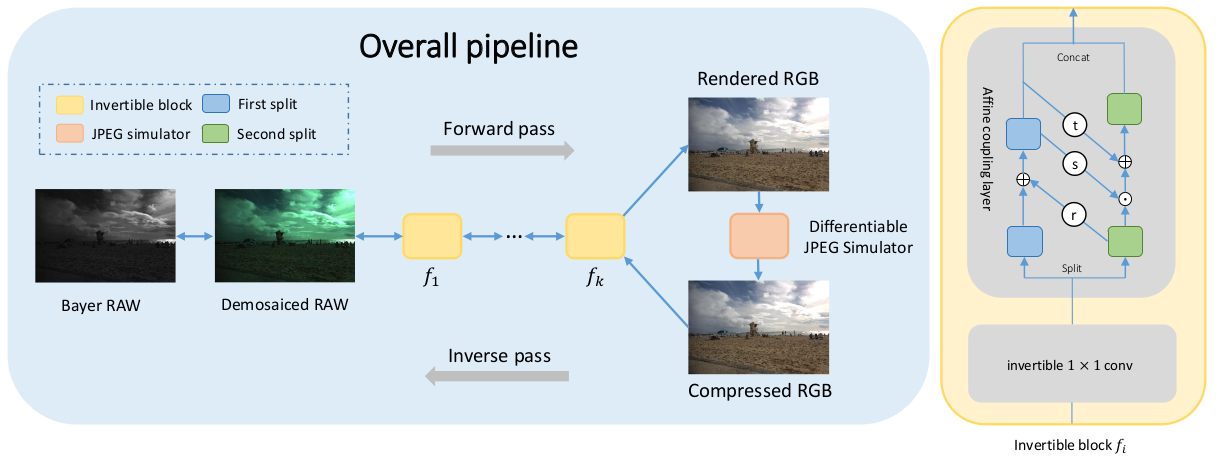Overall pipeline of the InvISP framework
The building block of the neural network is based on the affine coupling layer of the RealNVP.
An arbitrary function $r$ with second split as the prior is summed up to the first split of the affine coupling layer to increase expressivity of the model following IRN.
Also, an 1$\times$1 convolution layer is utilized as a learnable permutation function following Glow.
(Theoretical background of the affine coupling layer is not discussed in this post, but it is really worth knowing. NICE, RealNVP are some of the earliest papers that achieve invertibility of a neural network layer by turning its Jacobian determinant into a triangular matrix!)
Although the basic building block is merely a combination of known modules, novelty of the InvISP comes with the differentiable JPEG simulator.
The authors address that the JPEG compression is not invertible due to the quantization process, and replace the rounding function to a differentiable function based on the Fourier series:
\begin{equation}
Q(I) = I - \frac{1}{\pi} \sum\nolimits^{K}_{k=1}\frac{(-1)^{k+1}}{k}sin(2 \pi k I),
\end{equation}
where $I$ is the input map after splitting, and $K$ is the tradeoff hyperparameter.
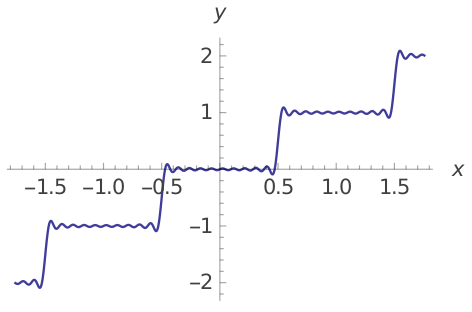Differentiable approximate rounding function
Now that the JPEG compression is differentiable, it can be incorporated into the backpropagation of the INN in an end-to-end manner.
Show qualitative and quantitative strengths over a few baseline models
First experiment demonstrates the quantiative performance (PSNR/SSIM) of the proposed method over other baselines.
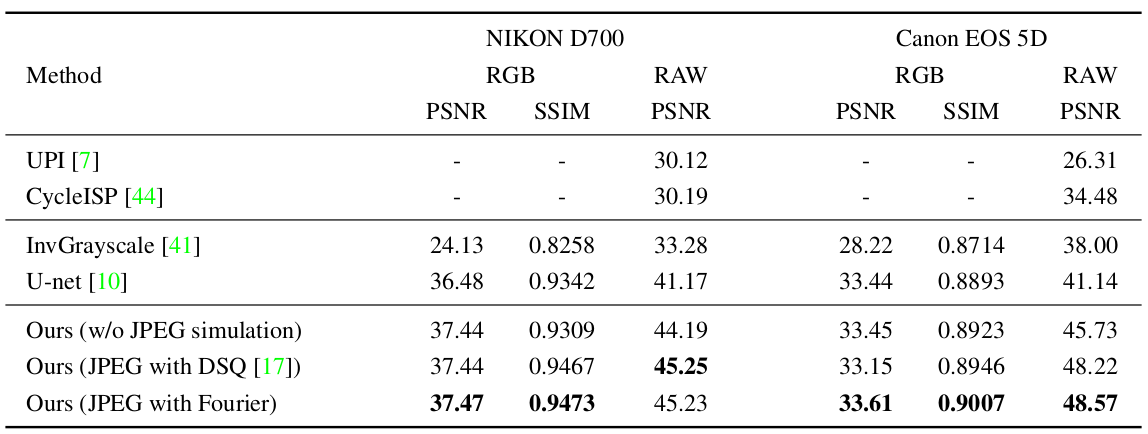Quantitative performance of the proposed method
Considering the invertibility of the proposed model, qualitative improvement of the JPEG to RAW can be a main strength of the proposed method.
The authors provide examples of qualitative improvement over UPI, CycleISP, Invertible Grayscale, and the U-net.
Qualitative improvement over SOTA methods, demonstrated by difference image
Qualitative improvement over baseline methods, demonstrated by difference image
For the proposed model to hold practical significance, the compression ratio should be at least comparable to that of the conventional RAW to RGB image processing followed by JPEG compression.
The authors show that the file size is remarkably reduced, even when compared with lossy DNG.
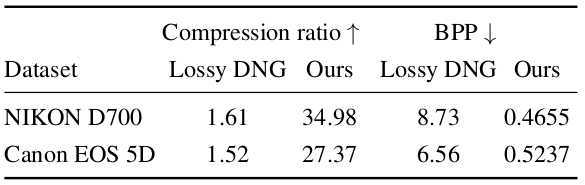Compression ratio of the proposed model
Related
- Palette: Image-to-Image Diffusion Models
- Deep reparameterization of Multi-Frame Super-Resolution and Denoising
- Hierarchical Conditional Flow: A Unified Framework for Image Super-Resolution and Image Rescaling
- Alias-Free Generative Adversarial Networks
- Clean Images are Hard to Reblur: A New Clue for Deblurring