[2106.12423] Alias-Free Generative Adversarial Networks

• Analyze equivariance of GAN operations from signal processing perspective
• Propose methods to introduce equivariance to the StyleGAN2 generator
• Show quantiatative and qualitative improvements over StyleGAN2 by experiments

Background

StyleGAN is well known for generating realistic high-resolution (1024 $\times$ 1024) images with progressive growing. Although StyleGAN is capable of generating high quality images, authors of this paper (who are also the authors of the StyleGAN and the StyleGAN2) address the issue of texture sticking. Texture sticking refers to the phenomenon that the generator memorizes a specific location within the pixel-grid to generate textural details of an image. This is an unwanted trend since an image generated from a fully disentangled latent space should be able to be semantically edited from a high-level context, not at a low-level pixel coordinate.

Texture sticking examples. Average of nearby latent codes should create blurry images of the central latent code if pixel coordinates are not memorized (left). Latent interpolation should smoothly vary at the same coordinates if textures are not memorized pixel-wise (right) Texture sticking can stem from lack of transformation equivariance in the operations of the neural network. The authors focus on translation and rotation equivariance of the StyleGAN2 generator to show that these equivariances are not fully achieved by the hierarchical convolutional architecture of the StyleGAN2 generator, and propose ways to introduce translation/rotation equivariance to the StyleGAN2 generator.

Keypoints

Analyze equivariance of GAN operations from signal processing perspective

The equivariance of the operations that comprise the generator is analyzed from the signal processing perspective. In particular, equivariance of convolution, up/downsampling, and nonlinearity are evaluated by its continuous counterparts. A spatial transformation $\mathbf{t}$ is equivariant if for an operation or signal $\mathbf{f}$ satisfies commutativity: \begin{equation} \mathbf{t} \circ \mathbf{f} = \mathbf{f} \circ \mathbf{t} \end{equation}

1. Convolution is translation equivariant, and further rotation equivariant if the kernel size is 1$\times$1.
2. Upsampling and downsmapling are translation equivariant, but rotational equivariance requires radially symmetric filter with disc-shaped frequency response.
3. Pointwise nonlinearity $\sigma$ in the discrete domain does not commute with translation/rotation, but does commute in the continuous domain.

Propose methods to introduce equivariance to the StyleGAN2 generator

Understanding the equivariance of generator operations is practically applied to the StyleGAN2. The goal is to make every layer of the generator equivariant with respect to the continuous signal. 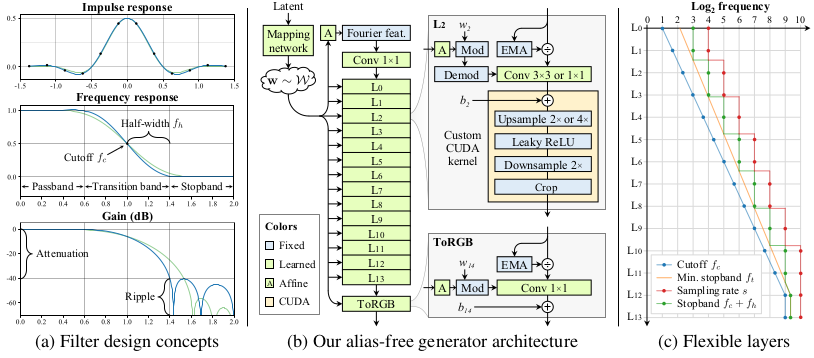Introducing equivariance to the StyleGAN2 generator

Practical solutions and their background can be summarized as:

1. Fourier features of learned input constant: facilitate exact continuous translation/rotation of the input with spatially infinite map
2. Baseline simplification: remove previous tricks not related to equivariance including per-pixel noise, mixing regularization, path length regularization, and output skip connections with smaller mapping network depth.
3. Extend boundary padding
4. Replace upsampling: Upsampling with better approximation of the ideal low-pass filter is possible with windowed $\mathrm{sinc}$ filter with large Kaiser window.
5. Filtered nonlinearity: upsample before leaky ReLU nonlinearity followed by downsampling better approximates continuous domain pointwise nonlinearity which is translation/rotation equivariant.
6. Non-critical sampling: Selecting appropriate filter cutoff near the bandlimit achieves better computational cost versus aliasing trade-off (left of above figure)
7. Transformed Fourier features: Learned affine transformation is applied to the input Fourier features to better introduce global transformations
8. Flexible layer spcifications (right of above figure).
9. Rotation equivariance: replacing 3$\times$3 convolutions with 1$\times$1 introduces rotation equivariance to convolution layers. $\mathrm{sinc}$ based downsampling is replaced with $\mathrm{jinc}$-based one. The final alias-free generator is illustrated in the middle of the above figure.

Show quantitative and qualitative improvements over StyleGAN2 by experiments

Each of the above practical solutions lead to improvement of image generation performance (lower FID) or better equivariance metrics (EQ-T for translation and EQ-R for rotation). 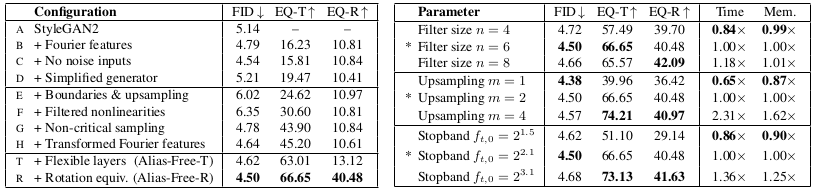Performance improvement with proposed configuration on StyleGAN2

The final alias-free generator architecture matches the FID score of the original StyleGAN2 with a bit higher computational cost for various datasets, including FFHQ-U (unaligned), FFHQ, MetFaces-U, MetFaces, AFHQv2, and Beaches. 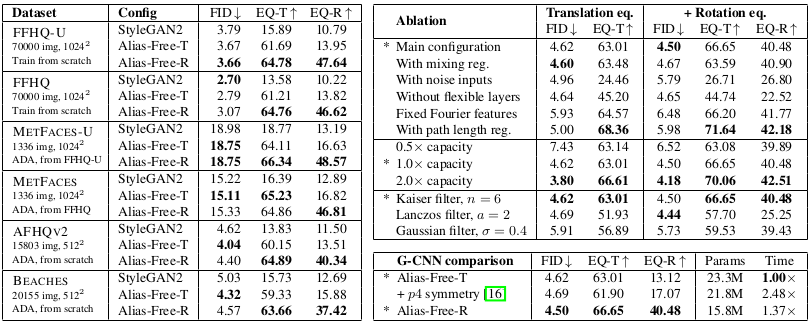Performance of the alias-free generator on various datasets It can be seen that the alias free generator shows better FID score for unaligned datasets when compared to the original StyleGAN2.

Feature representation of StyleGAN2 and alias free generators Interestingly, the internal representation of StyleGAN2 show that feature maps of all layers seem to encode signal magnitudes, while the some layers of the alias free generator encode phase information instead. This qualitative finding further supports the theoretical understanding of equivariance of the alias free generators. High-level representation without texture sticking would probably enable better generating / editing results when the model is extended to the video data.

• A Picture is Worth a Thousand Words: Principled Recaptioning Improves Image Generation
• Tackling the Generative Learning Trilemma with Denoising Diffusion GANs
• Image Synthesis and Editing with Stochastic Differential Equations
• RewriteNet: Realistic Scene Text Image Generation via Editing Text in Real-world Image
• ViTGAN: Training GANs with Vision Transformers