Significance
Keypoints
- Propose pruning framework for continuous normalizing flow
- Demonstrate density estimation performance and generalization of the pruned flow models
Review
Background
Normalizing flow is one of the generative models, which targets to map a complex data distribution to a known distribution with possible reversal with change-of-variables of the likelihood. Continuous normalizing flow (CNF) exploits neural ordinary differential equation (ODE) to enable learning flexible probabilistic models. Pruning refers to the algorithms that reduces the number of neurons/weights from a trained neural network (which also actually happens for developing brains). The authors propose a framework for pruning the well known CNF model, FFJORD, and show that pruning improves generalization and efficiency of the model.
Keypoints
Propose pruning framework for continuous normalizing flow
The authors sparsify the CNF model by removing redundant weights from the neural network during training with iterative learning rate rewinding, i.e. iteratively train a dense neural network and retrain with pruning until the desired level of sparsity is obtained.
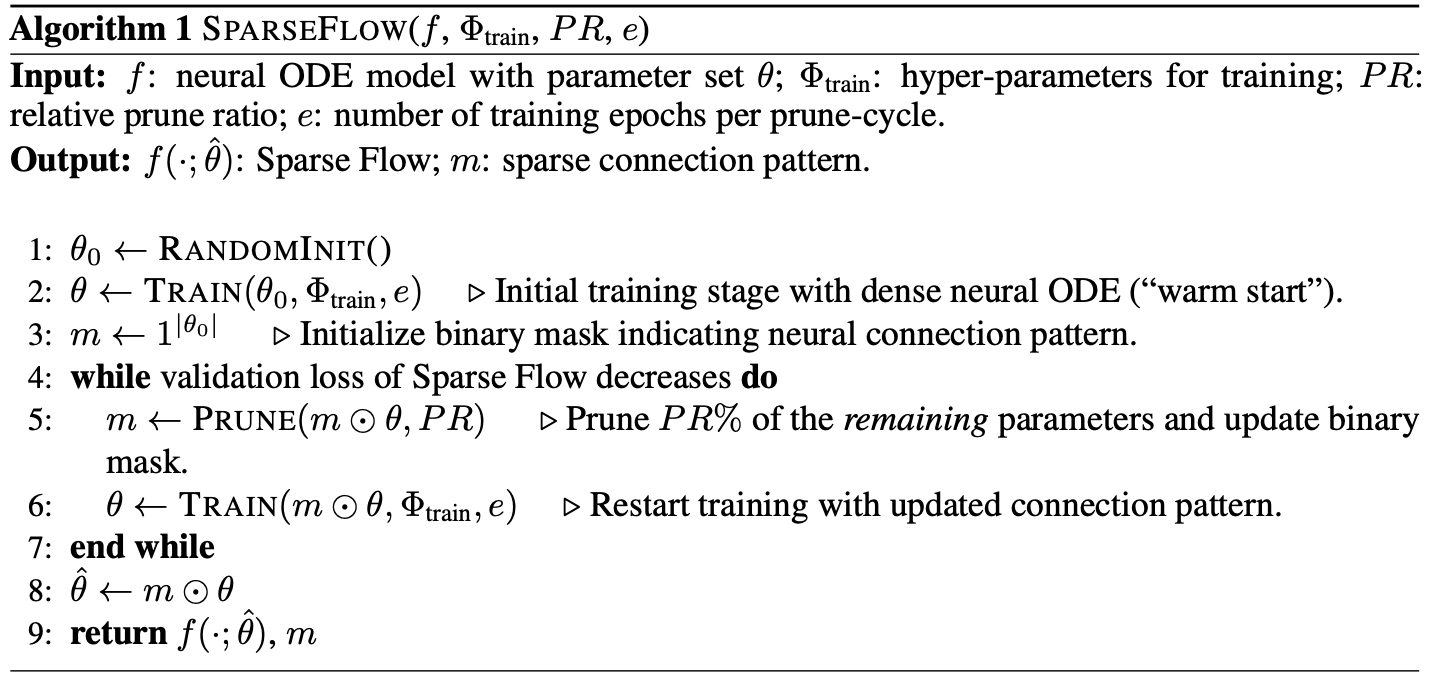Pseudocode of the proposed Sparse Flow
For the prune step at line 5 of the above pseudocode, both unstructured (weight pruning) and structured (neuron pruning) pruning are experimented.
Demonstrate density estimation performance and generalization of the pruned flow models
Density estimation of multimodal Gaussian placed orderly on a spiral and a spiral distribution with sparse regions was experimented.
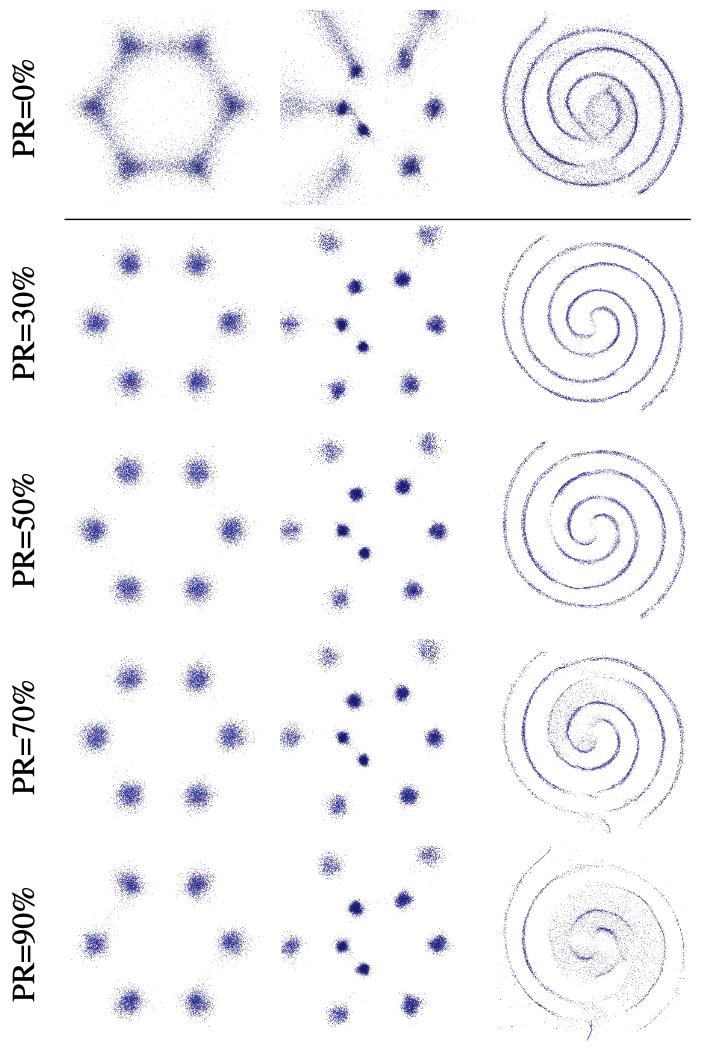Density estimation result with respect to prune ratio (PR)
It can be seen qualitatively that the quality of the density estimation improves by increasing prune ration (PR) to a certain level.
Negative Log Loss (NLL) with respect to prune ratio
This trend was also apparent in quantitative comparison where the negative log loss (NLL) is plotted with respect to the PR.
Inner dynamics of pruning is further explored by the vector-field constructed by the flow to model 6 Gaussians independently.
Inner dynamics of SparseFlow
It can be seen that SparseFlows attract the vector-field directions (especially PR=70%) uniformly toward the mean of each Gaussians, while the unpruned flow does not.
Density estimation on real tabular/image datasets also show that pruning the flow substantially improves performance and reduces number of parameters.
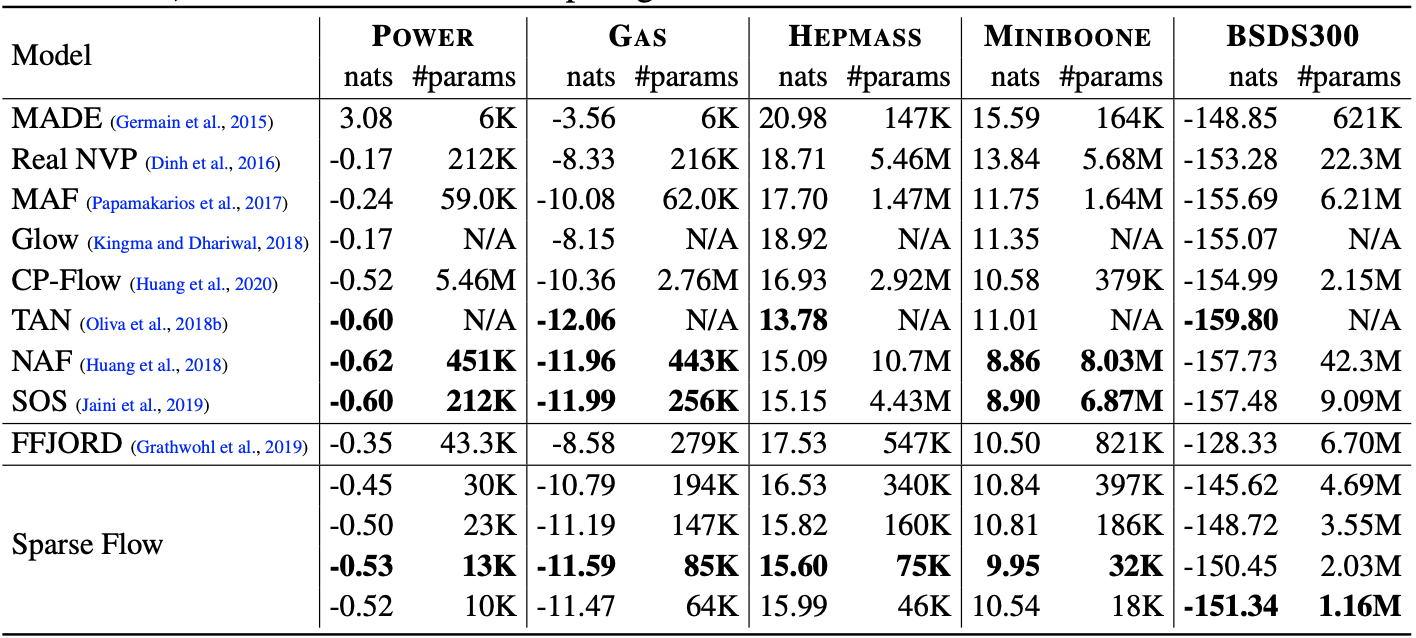Density estimation result on real tabular datasets
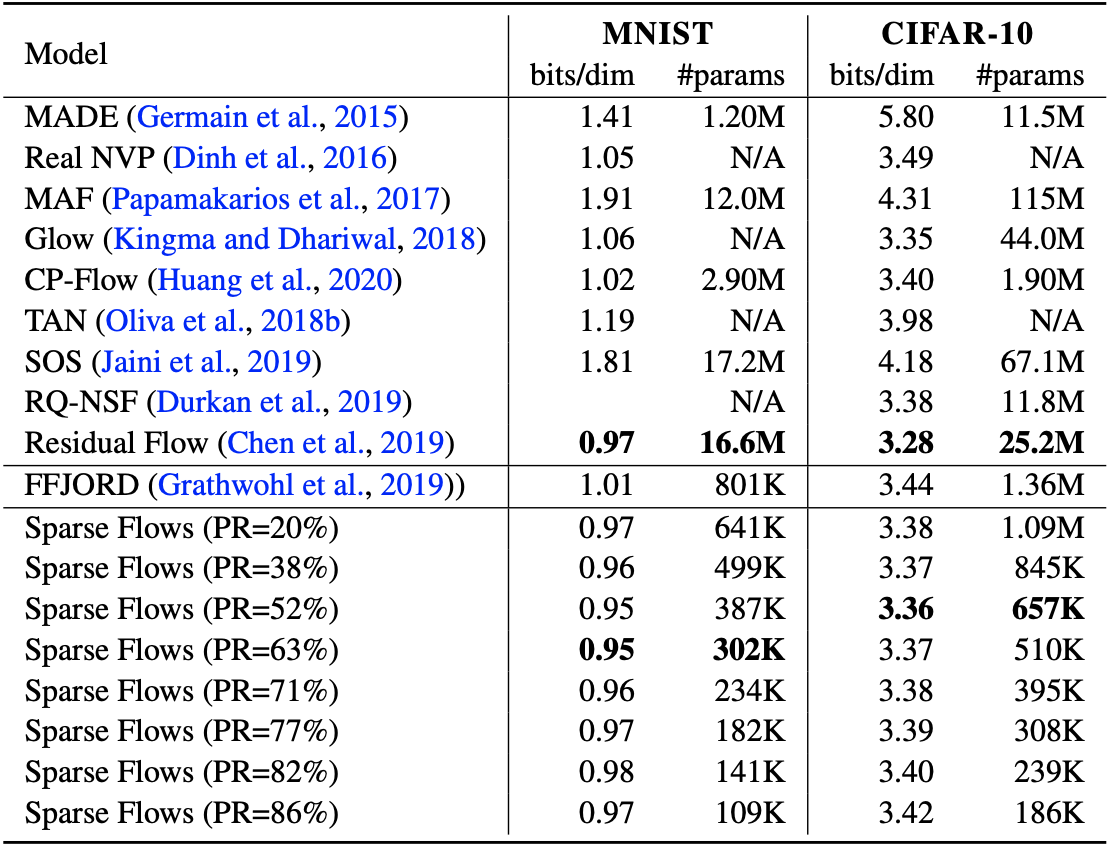Density estimation result on real image datasets
Improved generalization of the pruned CNFs can be partially explained by resolution of the mode-collapse.
The authors further investigate this property from the perspective of flat loss surface.
Flatness of the loss surface is evaluated by the largest eigenvalues, traces, and condition numbers of the Hessian.
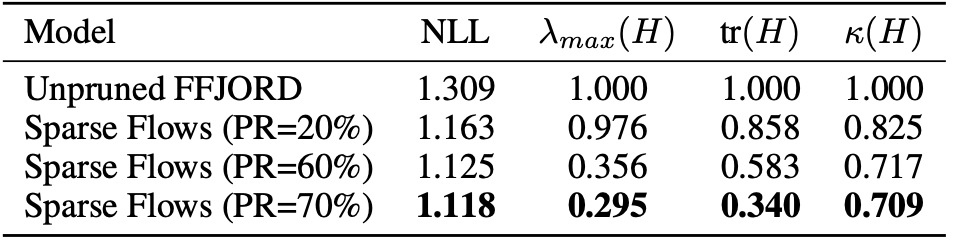Flatness of the loss surface by maximum eigenvalue $\lambda_{max}(H)$, trace $\mathrm{tr}(H)$, and condition number $\kappa (H)$
The values suggest that the loss surface becomes more flat as the generalization gets better (this interpretation may require caution since PR=90% is not shown).
Robustness study of the proposed Sparse Flow is referred to the original paper