Significance
Keypoints
- Propose a continuous normalizing flow incorporating multi-resolution approach
- Demonstrate quality and efficiency of the proposed method by experiments
Review
Background
Normalizing flow is one of the generative models, which targets to map a complex data distribution to a known distribution with possible reversal with change-of-variables of the likelihood. Although practical application of normalizing flows have been limited due to its relative underperformance compared to GANs and VAEs, normalizing flows are still attractive in that they enable density estimation and computation of exact likelihoods. Continuous normalizing flow (CNF) is a continuous time variant of normalizing flow which uses Neural ODEs, and they have shown promising results in image generation. The authors propose to incorporate multi-resolution approach to the CNF to improve its generated image quality and efficiency.
Keypoints
Propose a continuous normalizing flow incorporating multi-resolution approach
The idea of multi-resolution approach for CNF is not new.
Applying wavelet decomposition to construct the image pyramid for training the normalizing flow has already been studied.
However, this work further extends this idea to the CNF and propose a non-trivial wavelet transform by modifying the Haar wavelet transform into an unimodular, volume-preserving one.
This transformation is represented by the matrix $M$:
\begin{align}
\begin{bmatrix} x_{1} \\ x_{2} \\ x_{3} \\ x_{4} \end{bmatrix} = \frac{1}{a} \begin{bmatrix} c c c a \\ c -c -c a \\ -c c -c a \\ -c -c c a \end{bmatrix} \begin{bmatrix} y_{1} \\ y_{2} \\ y_{3} \\ \bar{x} \end{bmatrix} \Longleftrightarrow \begin{bmatrix} y_{1} \\ y_{2} \\ y_{3} \\ \bar{x} \end{bmatrix} = \begin{bmatrix} c^{-1} c^{-1} -c^{-1} -c^{-1} \\ c^{-1} -c^{-1} c^{-1} -c^{-1} \\ c^{-1} -c^{-1} -c^{-1} c^{-1} \\ a^{-1} a^{-1} a^{-1} a^{-1} \end{bmatrix} \begin{bmatrix} x_{1} \\ x_{2} \\ x_{3} \\ x_{4} \end{bmatrix},
\end{align}
where $x_{i}$ is the image pixel at index $i$, $\bar{x}$ is the low frequency image, $y_{j}$ is the high frequency detail, $c=2^{2/3}$, $a=4$, and $\log |\det(M^{-1})| = \log (1) =0$.
Now, the volume-preserving multi-resolution process with scaling can be constructed without loss of signal by
\begin{align}
\mathbf{x}_{s} = M(\mathbf{y}_{s}, \mathbf{x}_{s+1}) \Longleftrightarrow \mathbf{y}_{s}, \mathbf{x}_{s+1} = M^{-1}(\mathbf{x}_{s}).
\end{align}
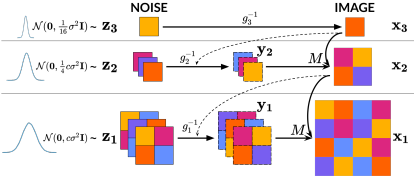Schematic illustration of the proposed method
At each level $s$, the high frequency detail counterparts $\mathbf{y}_{s}$ and the low frequency image at the lowest resolution $\mathbf{x}_{S}$ are generated by training a CNF.
This idea reminded me of my approach for the extreme (x16) image super-resolution challenge to generate a pyramid of wavelet details to consecutively upscale an image (see my solution github repo).
Demonstrate quality and efficiency of the proposed method by experiments
Image quality generated by the proposed multi-resolution continuous normalizing flow (MRCNF) is experimented on the CIFAR-10 and the ImageNet dataset with 32$\times$32 / 64$\times$64 resolution.
The bits-per-dimension (BPD $\downarrow$) and the training time in GPU hours are compared with various flow-based and non-flow-based generative models.
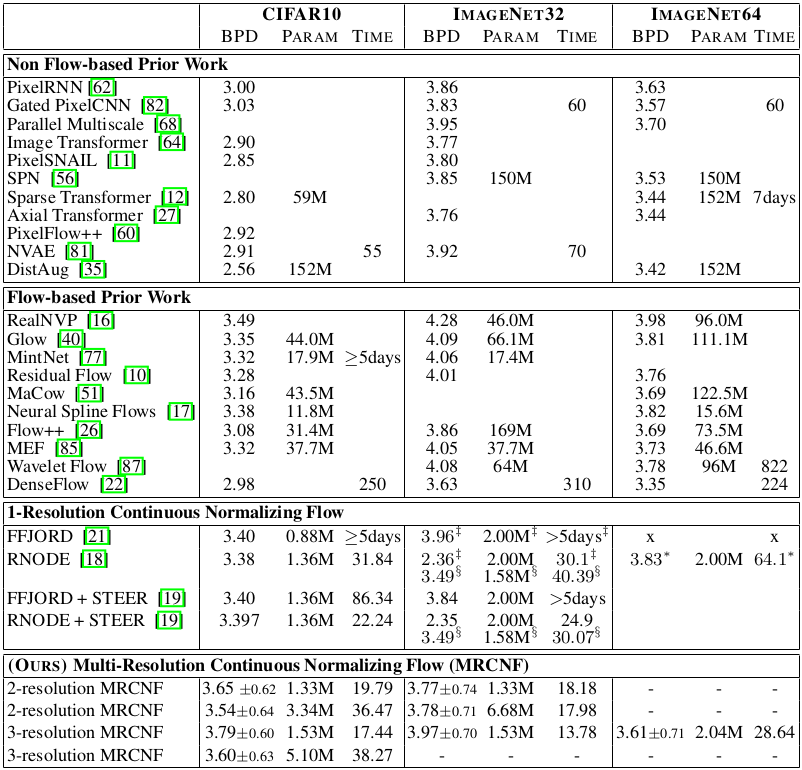Comparative study results of the proposed method
Qualitative results of the proposed method on CIFAR-10 dataset
Although the quantitative results are not satisfying for the low-resolution data, proposed MRCNF performs better than the 1-resolution FFJORD for the 64$\times$64 resolution.
Higher-resolution (128$\times$128) images was also generated by progressive training and showed comparative performance with small number of paramters.
Progressive training at 128$\times$128 ImageNet data
Experiments on applying MRCNF to out-of-distribution data are referred to the original paper.
I personally thought that it would have been more interesting if the MRCNF was tested on even higher resolutions, like 1024$\times$1024 and the performance was compared with GANs and VAEs.
However, this work still suggests an important direction in improving the flow-based models.
Related
- A Picture is Worth a Thousand Words: Principled Recaptioning Improves Image Generation
- Tackling the Generative Learning Trilemma with Denoising Diffusion GANs
- Hierarchical Conditional Flow: A Unified Framework for Image Super-Resolution and Image Rescaling
- Image Synthesis and Editing with Stochastic Differential Equations
- RewriteNet: Realistic Scene Text Image Generation via Editing Text in Real-world Image