[2108.06098] FedPara: Low-rank Hadamard Product Parameterization for Efficient Federated Learning

• Propose a low-rank Hadamard product based weight matrix decomposition for efficient federated learning
• Demonstrate efficiency and performance of the proposed method by experiments

Background

Federated learning is a server-centered machine learning framework that does not require sharing local data between clients (or parties), keeping it safe from potential security/privacy issues. The federated learning process usually takes steps of (1) distributing the global model to local parties, (2) training the model locally with data on each party, (3) sending the trained model back to the server, and (4) aggregating the collected local models to update the global model. Therefore, the model parameters should be downloaded/uploaded at each training rounds in every edge devices which can be an important problem with limited bandwidth. This work addresses this issue and propose low-rank Hadamard product parameterization to reduce number of parameter elements and enhance efficiency in federated learning.

Keypoints

Propose a low-rank Hadamard product based weight matrix decomposition for efficient federated learning

Given that a weight matrix matrix $\mathbf{W} \in \mathbb{R}^{m\times n}$ is low-rank with $\mathrm{rank}(\mathbf{W})\leq 2R$, it can be decomposed into the multiplication of two matrices $\mathbf{X} \in \mathbb{R}^{m \times 2R}$ and $\mathbf{Y} \in \mathbb{R}^{2R \times n}$ such that $\mathbf{W} = \mathbf{X}\mathbf{Y}^{\top}$. The proposed FedPara takes a similar low-rank decomposition but incorporates Hadamard product of two decomposed matrices to improve expressiveness of the neural network while maintaining small number of parameters. More specifically, the weight matrix $\mathbf{W}$ with $\mathrm{rank}(\mathbf{W})\leq R^{2}$ is decomposed into $\mathbf{W} = \mathbf{W}_{1} \odot \mathbf{W}_{2} = (\mathbf{X}_{1}\mathbf{Y}_{1}^{\top}) \odot (\mathbf{X}_{2}\mathbf{Y}_{2}^{\top})$ where $\mathbf{X}_{1}, \mathbf{X}_{2} \in \mathbb{R}^{m \times R}$ and $\mathbf{Y}_{1}, \mathbf{Y}_{2} \in \mathbb{R}^{R \times n}$

Schematic illustration of the low-rank Hadamard product decomposition used in FedPara

Hadamard product of FedPara is extended to personalization FedPara (pFedPara), where the Hadamard product acts as a bridge between the global inner weight $\mathbf{W}_{1}$ and the local inner weight $\mathbf{W}_{2}$. In other words, weight $\mathbf{W}_{1}$ is transferred to the server while $\mathbf{W}_{2}$ is kept local, which increases the communication efficiency further.

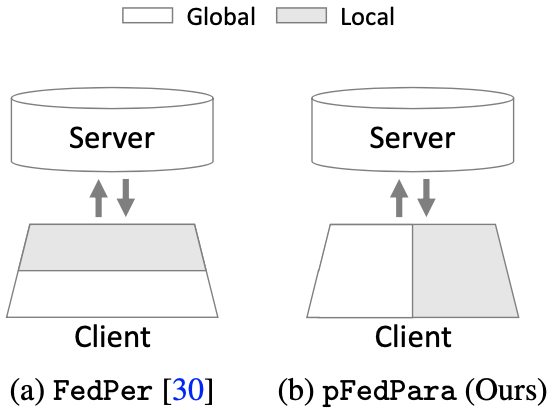Schematic illustration of the pFedPara

Demonstrate efficiency and performance of the proposed method by experiments

Performance and efficiency of the proposed FedPara and pFedPara are experimented with federated VGG models (VGGorig: VGG original; VGGlow: low-rank decomposed) on the CIFAR-10, CIFAR-100 and CINIC-10 datasets. 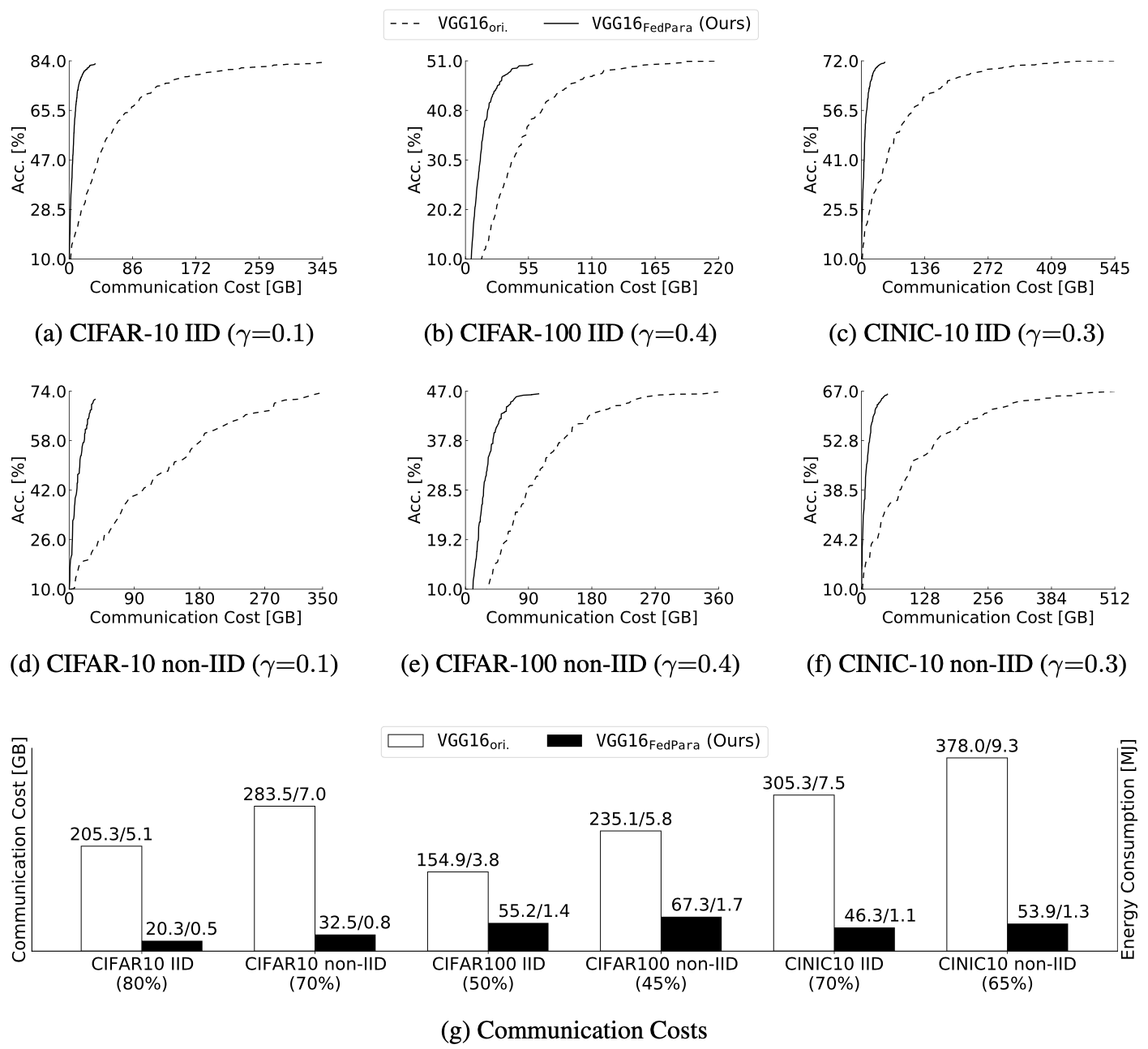Accuracy vs. cost of the proposed method

It can be seen that the proposed FedPara has significantly lower communication cost with comparable accuracy.

Accuracy of the proposed method in specific target rounds (T)

The accuracy of the proposed FedPara outperforms low-rank decomposed VGG when the target rounds are matched.

Further comparative experiment results and pFedPara performance are referred to the original paper

• Recurrent Parameter Generators
• Orthogonalizing Convolutional Layers with the Cayley Transform
• Model-Contrastive Federated Learning