Significance
Keypoints
- Propose a method that uses Cayley transform to make a convolution layer orthogonal
- Demonstrate orthogonality and improvement in adversarial robustness of the proposed method
Review
Background
A square orthogonal matrix $A$ which satisfies $A^{\top}A=AA^{\top}=I$ can be thought as a norm-preserving linear transformation function. It can be intuitively thought that the neural network with orthogonal weights may possess a more stable property, owing to this norm-preserving property. Empirical results also suggest that this is true, showing better generalization or improved adversarial robustness for neural networks that encourage orthogonality, However, enforcing orthogonality of a convolution layer has not been studied as much as it has been done for a fully-connected layer. Methods that constrain Lipschitz constants of convolution layers by minimizing the upper bound loosely impose norm-preserving property, but still leaves room for improvement. The authors aim to provide a direct parametrization of orthogonal convolution by introducing Cayley transformation to the convolution layer, which can be generalized to the layer with a non-square weight matrix.
Keypoints
Propose a method that uses Cayley transform to make a convolution layer orthogonal
Things that you need to know to understand the proposed algorithm are:
- Any square matrix $B$ can be made skew-symmetric by computing $B-B^{\top}$
- Cayley transform $(I+A)(I-A)^{-1}$ bijectively maps a skew symmetric matrix $A$ to an orthogonal matrix, and vice versa
- Convolution in the spatial domain corresponds to element-wise product in the Fourier domain (the convolution theorem)
Now, a convolution layer weight $W$ can be made skew-symmetric by $W-W^{\top}$, and further be made orthogonal by the Cayley transform of this skew-symmetric matrix (Here, the convolution is assumed to be circular for mathematical simplicity).
However, the Cayley transform requires computing inverse of $(I-A)$, which the authors note that inverting the convolution is not very efficient.
Since the inverse can be computed in the Fourier domain as an efficient matrix-vector product, the authors alternatively perform convolution of the orthogonal matrix in the Fourier domain.
After the convolution with orthogonalized weight is done, inverse Fourier transform is applied to obtain the final layer output.
The process is be summarized in the following pseudocode.
Pseudocode of the proposed orthogonal convolution
This orthogonal convolution is explicitly orthogonal and does not require additional parameters, but has limitations in computational efficiency (compared to vanilla convolution), need for indirect striding, and assumption of circular convolution.
Demonstrate orthogonality and improvement in adversarial robustness of the proposed method
The experiments have two objectives. First is to demonstrate whether the proposed convolution layer actually stays orthogonal. To confirm orthogonality, the authors instead show that proposed convolution $\texttt{CayleyConv}(X)$ with input $X$ is norm preserving: i.e. ($||\texttt{CayleyConv}(X)||_{2} / ||X||_{2} \approx 1$)
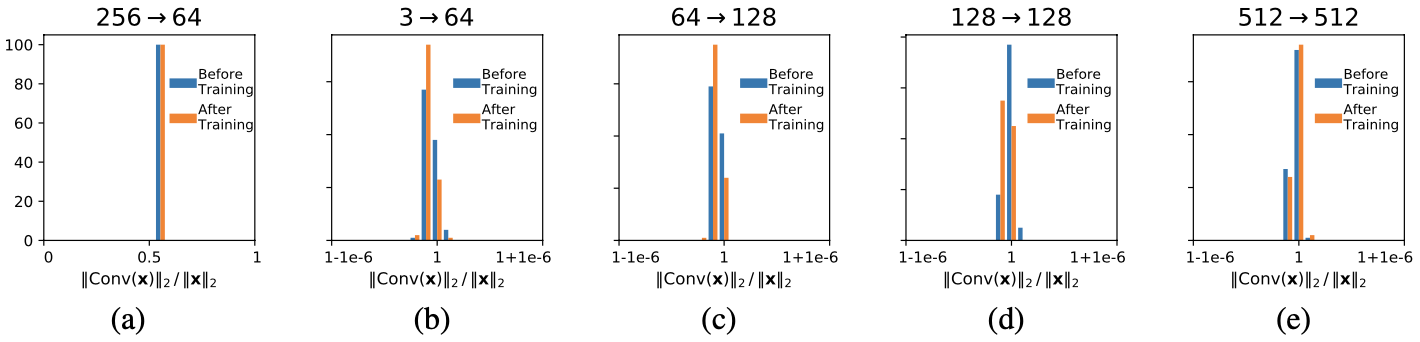Proposed convolution is mostly orthogonal irrespective of the number of input/output channels
Second objective is to demonstrate improved adversarial robustness.
With the proposed Cayley convolution, deterministic certifiable robustness is improved when compared to BCOP, RKO (Reshaped kernel orthogonalization), CRKO (Cayley RKO), OSSN (One-sided spectral normalization), and SVCM (Singular value clipping method).
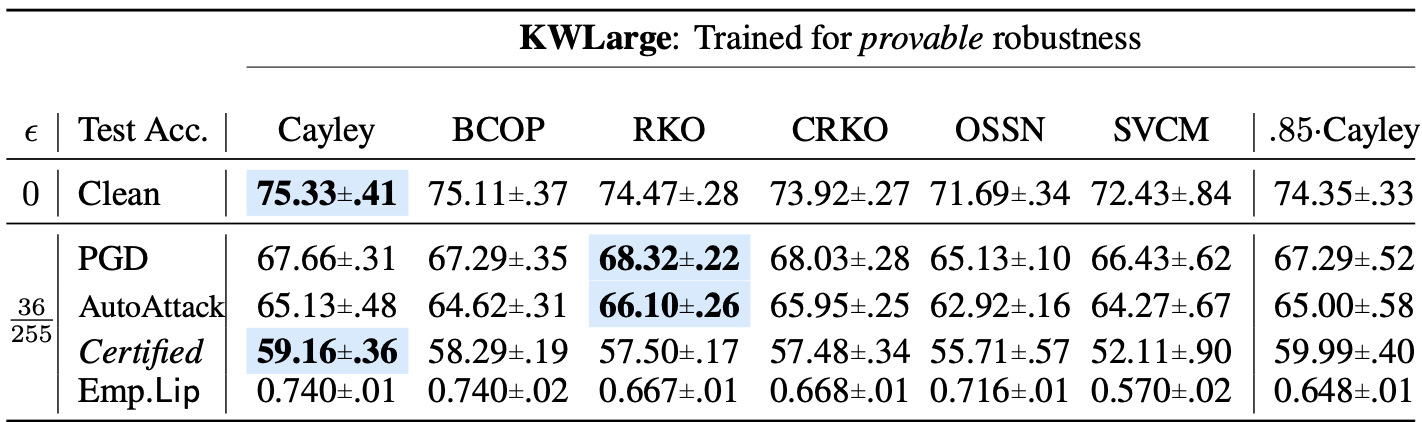Performance on provable robustness
Empirical robustness on $l_{2}$ gradient-based adversary is also tested on the ResNet9 and WideResNet10-10, showing better classification accuracy.
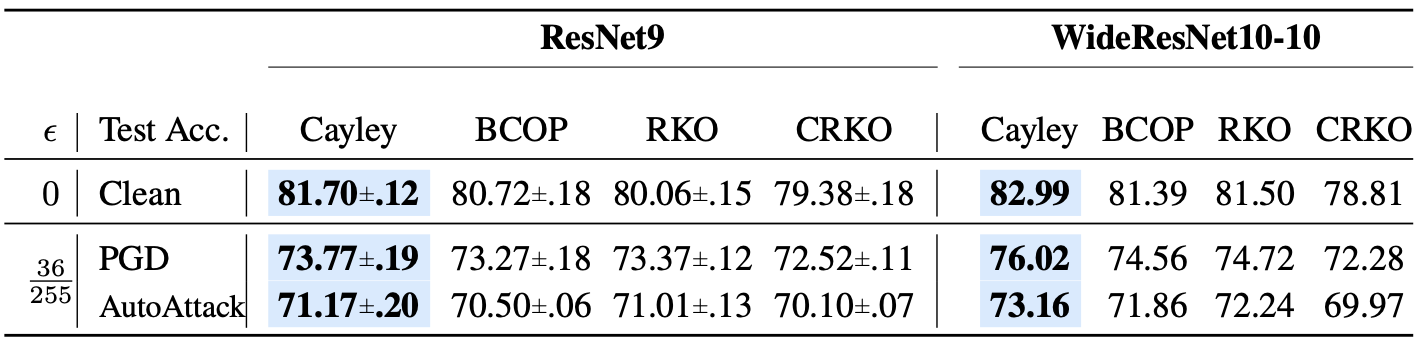Performance on empirical robustness
Although further mathematical details on the proposed method is available in the appendices of the original work, the core idea still comes from the three things discussed at the beginning of this section.