Significance
Keypoints
- Propose a loss function that enforces inter-class orthogonality in the feature space
- Confirm performance improvement by extensive experiments
Review
Background
Cross-entropy loss is a common choice of option when training a deep neural network for classification tasks. Variants of the cross-entropy loss, such as the angular margin based losses, have been studied to enhance its performance by improving discriminability of the feature space. This work also aims to improve the cross-entropy loss by enforcing inter-class separation and intra-class clustering without introducing any additional learnable parameters.
Keypoints
Propose a loss function that enforces inter-class orthogonality in the feature space
Training with cross-entropy loss implicitly achieves inter-class orthogonality of the features if the ground-truth labels are encoded as one-hot vectors (which are orthogonal). The key idea of the authors is to enforce this inter-class orthogonality more explicitly by adding a simple and straightforward loss function to the cross-entropy loss. The orthogonal projection loss $\mathcal{L}_{\texttt{OPL}}$ is defined as
\begin{align} s &= \sum_{i,j \in B , y_{i} = y_{j}} \langle \mathbf{f}_{i}, \mathbf{f} _{j} \rangle \\ d &= \sum_{i,k \in B , y_{i} \neq y_{k}} \langle \mathbf{f}_{i}, \mathbf{f} _{k} \rangle \\ \mathcal{L}_{\texttt{OPL}} &= (1-s) + |d|\label{opl} \end{align}
where $y$ is the class label and $\mathbf{f}$ is the intermediate feature of the neural network with subscript $i$, $j$, $k$ are indices within the minibatch $B$.
It should be noted that the bracket notation $\langle \cdot , \cdot \rangle$ denotes cosine similarity in this paper, not the inner product between the two vectors.
The orthogonal projection loss drags the cosine similarity of the same class samples $s$ towards 1 (i.e., linear dependence between the two vectors) and the cosine similarity of the different class samples $d$ towards 0 (i.e., orthogonality between the two vectors).
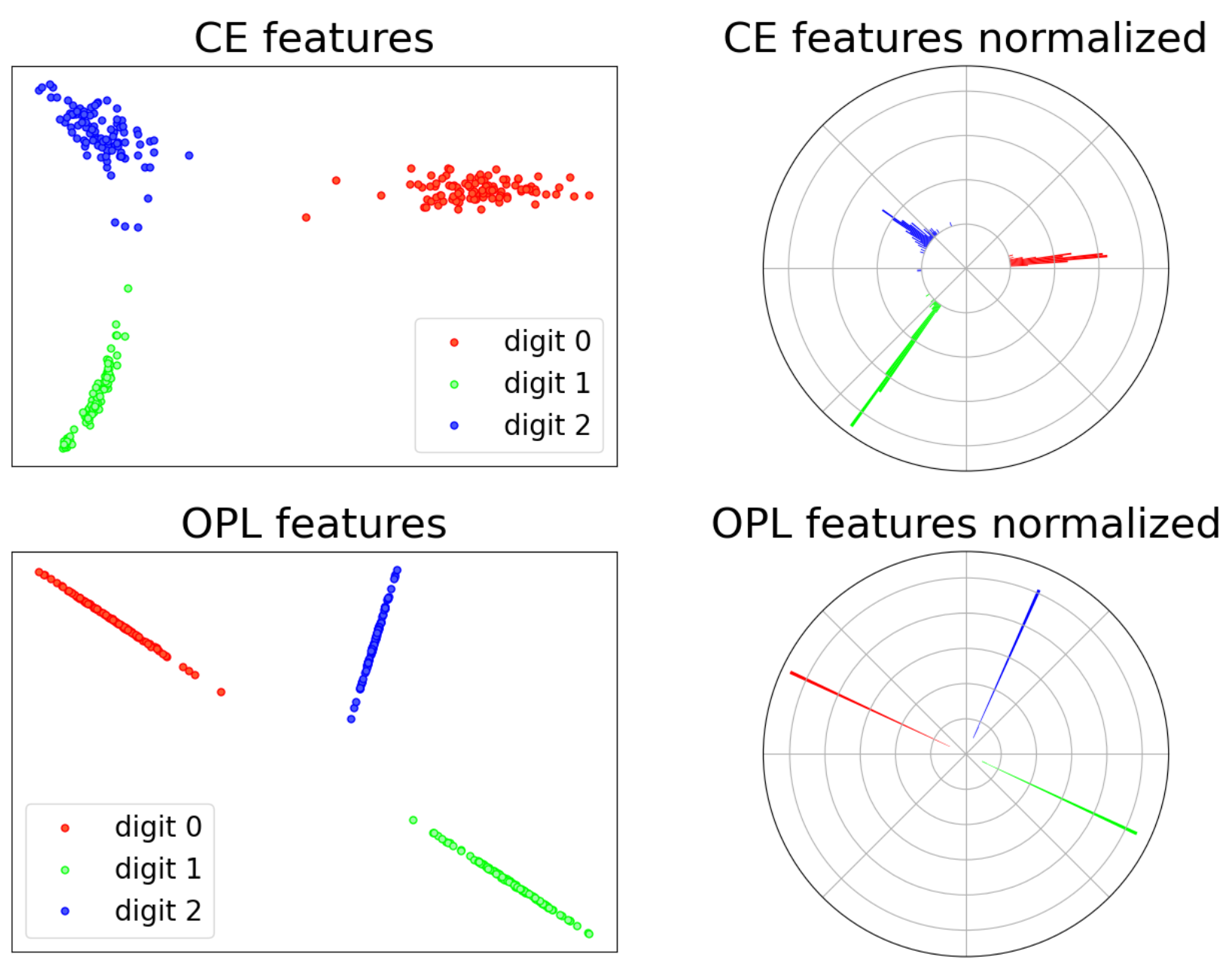Cross-entropy loss implicitly achieves orthogonality. Adding orthogonal projection loss can further achieve this explicitly.
This inter-class orthogonality and intra-class clustering is expected to improve the performance of the trained neural network.
In practice, the importance of $d$ with respect to $s$ is controlled by introducing a hyperparameter $\gamma$, reformulating the equation \eqref{opl} to \begin{align} \mathcal{L} _ {\texttt{OPL}} = (1 - s) + \gamma * |d|. \end{align}
Confirm performance improvement by extensive experiments
Improvement in performance is confirmed by extensive experiments, including image classification task, robustness against label noise, robustness against adversarial attacks and generalization to domain shifts.
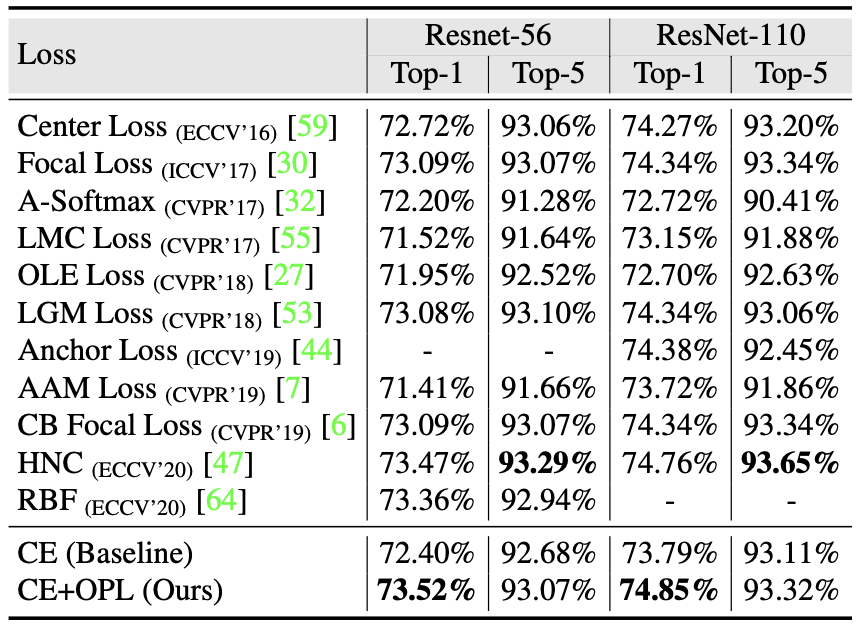
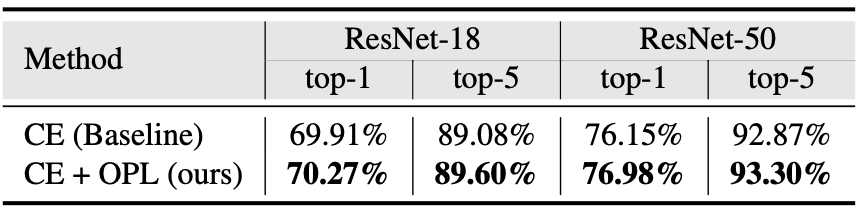Image classification task using CIFAR-100 and ImageNet dataset
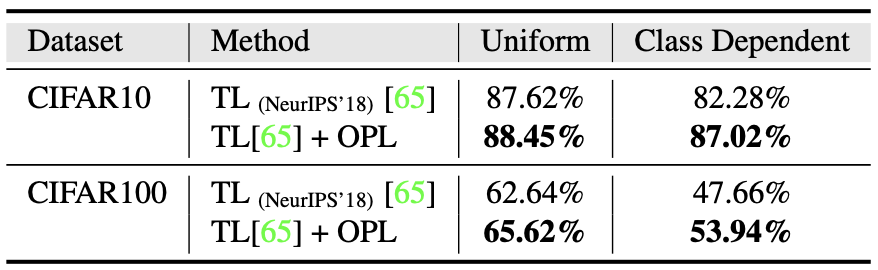Label noise robustness
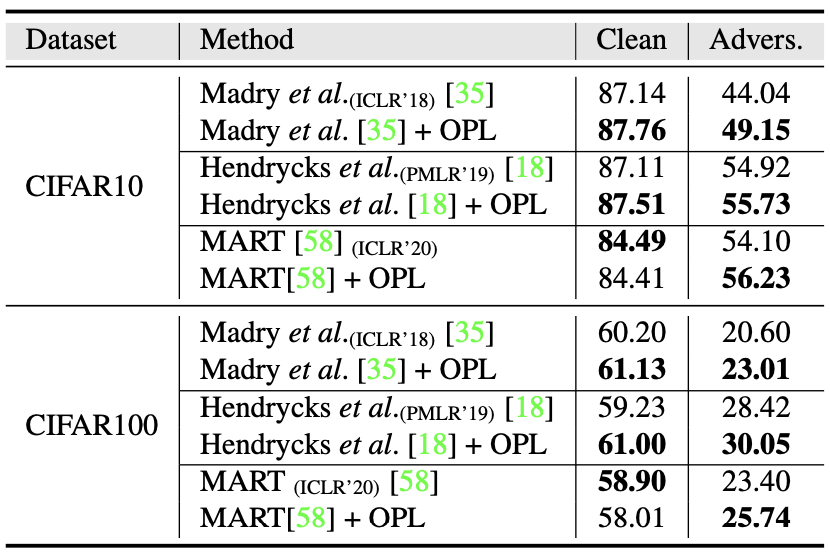Adversarial robustness
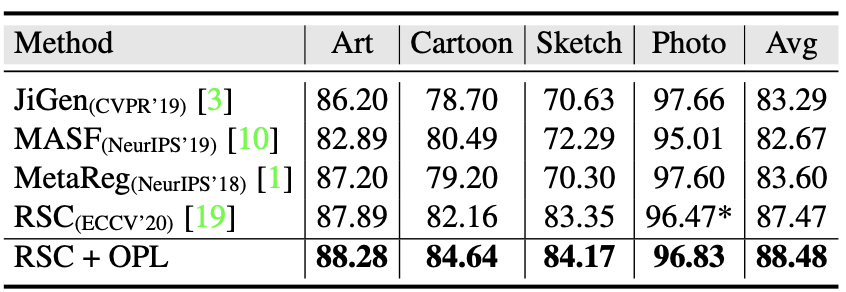Generalization to domain shifts
The authors further observe that transferability is enhanced in the case of of orthogonal features.
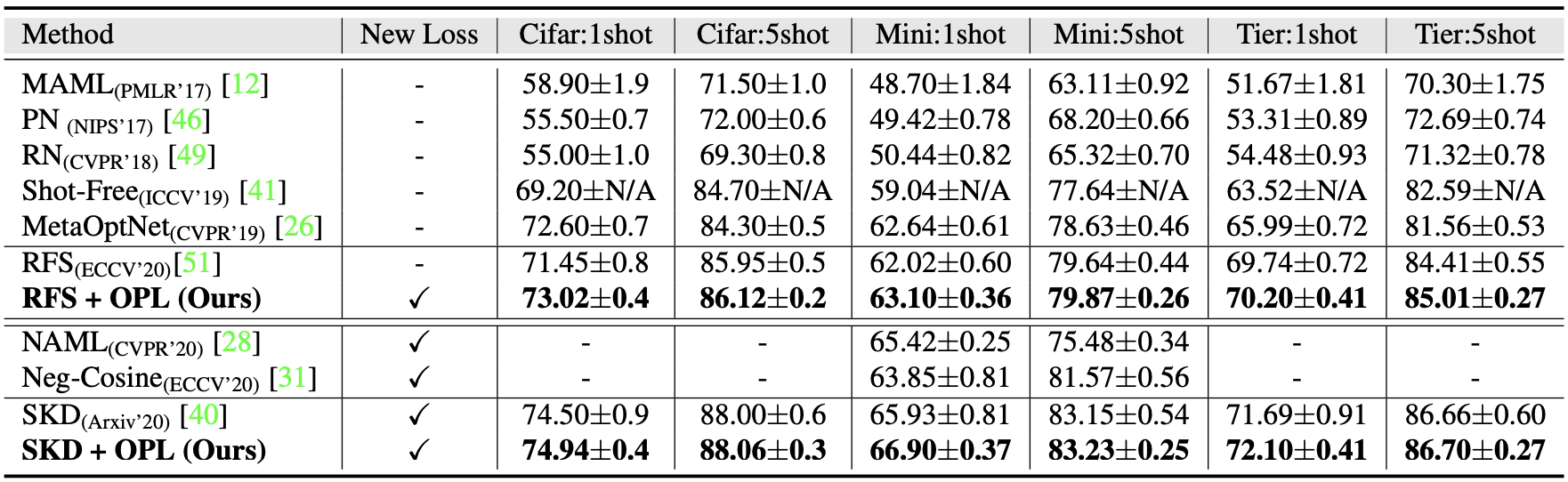Transferability in few-shot learning