Significance
Keypoints
- Propose an objective function that encourages domain generalization
- Improve computational efficiency of the proposed method by numerical approximation
- Demonstrate performance of the proposed method for unseen domain generalization
Review
Background
For a trained neural network to generalize better to a previously unseen domain, inference of the neural network should be based on invariant features across the domain, while ignoring spuriously correlated features. Assume that the goal of our neural network model is to classify the images of camels or cows. If our model has learned to make decision from the characteristics of the animal (invariant features), then it can have a better chance at generalizing to unseen class of animals than when it has learned to make decision from the background textures (sand or grass: spuriously correlated features). Numerous studies that try to address the domain generalization problem have been motivated by encouraging this invariances across domains. This work is in line with this idea, and propose an objective that can make models to learn invariant gradient direction for different domains during training. $\sim$
Keypoints
Propose an objective function that encourages domain generalization
We first formally define the domain generalization problem.
For the training dataset $\mathcal{D}_{train}$ with $S$ domains $\mathcal{D}_{train} = \{ \mathcal{D}_{1}, …, \mathcal{D}_{S}\}$, input-label pair exists for each domain $s$: $\mathcal{D}_{s}:= \{(x^{s}_{i},y^{s}_{i})\}^{n_{s}}_{i=1}$.
The test dataset $\mathcal{D}_{test} = \{\mathcal{D}_{S+1},…\mathcal{D}_{S+T}\}$ consists of $T$ domains where $\mathcal{D}_{train} \cap \mathcal{D}_{test} = \emptyset$.
Now, the domain generalization problem is to find the parameter $\theta$ of the neural network model such that:
\begin{equation}\label{eq:domain_generalization}
\underset{\theta}{\arg\min}\mathbb{E}_{\mathcal{D}\sim\mathcal{D_{test}}}\mathbb{E}_{(x,y)\sim\mathcal{D}}[ l((x,y);\theta)],
\end{equation}
where $l((x,y);\theta)$ is the loss of model $\theta$ on $(x,y)$.
The empirical risk minimization (ERM) refers to a naive approach for solving \eqref{eq:domain_generalization} minimizing the average loss on the training dataset $\mathcal{D}_{train}$, which is usually done for training a neural network in practice:
\begin{equation}\label{eq:erm}
\mathcal{L}_{\text{erm}}(\mathcal{D}_{train};\theta) = \mathbb{E}_{\mathcal{D}\sim\mathcal{D_{train}}}\mathbb{E}_{(x,y)\sim\mathcal{D}}[l((x,y);\theta)].
\end{equation}
The authors show that ERM approach can fail on domain generalization problems by focusing on spurious correlations with a simple example, which the details are referred to the original paper.
To address this issue of ERM, the gradients of the two different domains for optimizing the neural network should point in a similar direction:
\begin{equation}\label{eq:gradients}
G_{1} = \mathbb{E}_{\mathcal{D}_{1}}\frac{\partial l((x,y);\theta)}{\partial\theta}, \quad G_{2} = \mathbb{E}_{\mathcal{D}_{2}}\frac{\partial l((x,y);\theta)}{\partial\theta}.
\end{equation}
Maximizing the inner product between the two vectors can imply that the direction of the two vectors are encouraged to be similar.
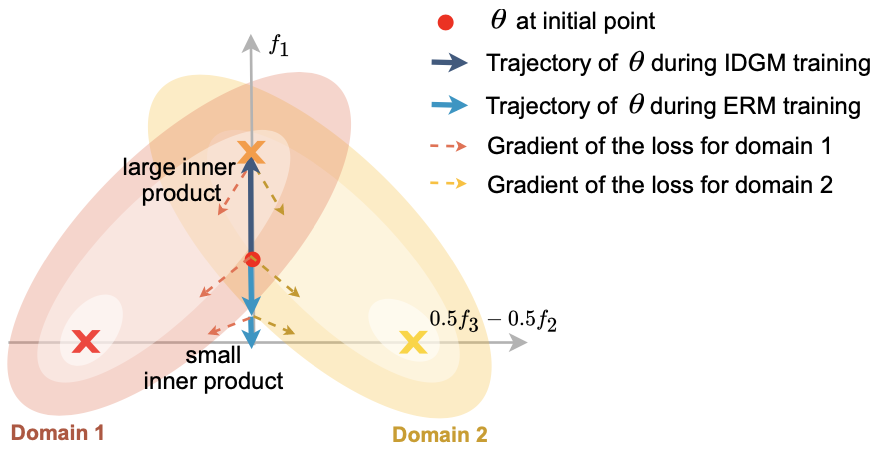Illustration of gradient direction and inner product of two different domains
The Inter-domain Gradient Matching (IDGM) is proposed exploiting this observation, which is an objective that is directly formulated as the inner product between the gradients of different domains: \begin{equation}\label{eq:idgm} \mathcal{L}_{\text{idgm}} = \mathcal{L}_{\text{erm}}(\mathcal{D}_{train};\theta) - \gamma \frac{2}{S(S-1)} \sum\nolimits^{i \neq j}_{i,j \in S} G_{i} \cdot G_{j}, \end{equation} where the second term of the right hand side is the Gradient Inner Product (GIP), computed as $||\sum_{i}G_{i}||^{2}-\sum_{i}||G_{i}||^{2}$ in practice.
Improve computational efficiency of the proposed method by numerical approximation
Since computing the GIP requires computing the second-order derivatives of the model parameters, the authors propose to improve computational efficiency of the IDGM by numerical approximation.
Based on a first-order algorithm Fish, the optimization of $\mathcal{L}_{\text{idgm}}$ is approximated efficiently in the inner-loop update.
Pseudocode of Fish approximation and its application to the IDGM
Theoretical justification of the approximation algorithm is referred to the original paper.
Demonstrate performance of the proposed method for unseen domain generalization
The performance of the proposed method is demonstrated with the CdSprites-N dataset, which is an extension of the dSprites dataset with color features and $N$ domains.
Samples of the CdSprites-N dataset
Evaluation of the domain generalization performance is done by changing $N$ from small to large values, with an assumption that domain generalization is more difficult for small $N$ since invariance cannot be learned sufficiently while chance of spurious correlations are higher.
The results show that Fish and Direct IDGM methods outperform ERM for the test set when the number of domain $N$ is small, suggesting better domain generalization performance of the proposed IDGM.
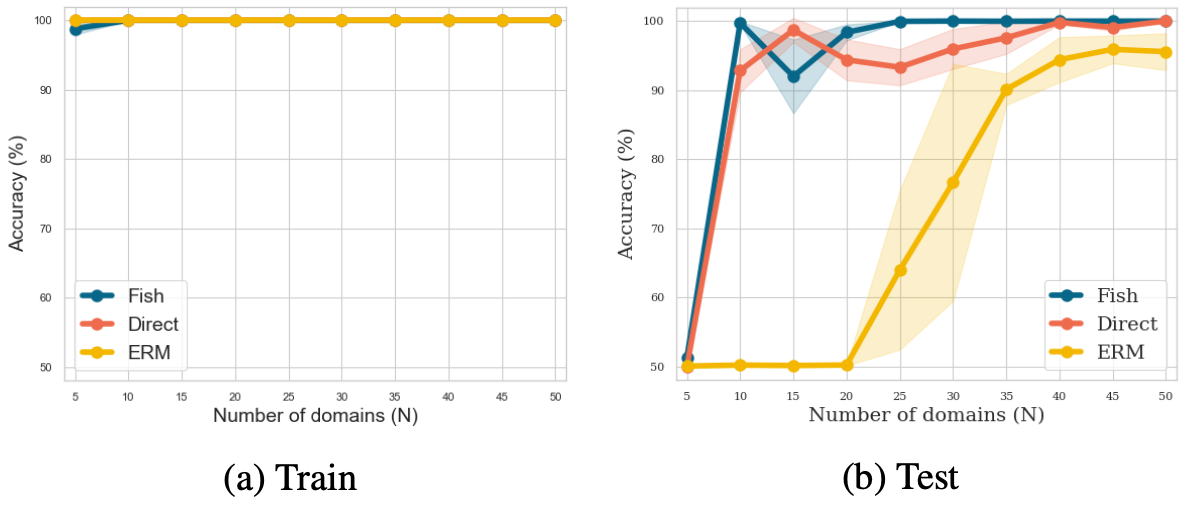Performance of the Fish/Direct IDGM on CdSprites-N dataset
The authors demonstrate similar results on the Wilds dataset for in-the-wild domain shifts.
To confirm the theoretical background of the proposed method with experiments, GIP of the ERM and the IDGM are compared during training.
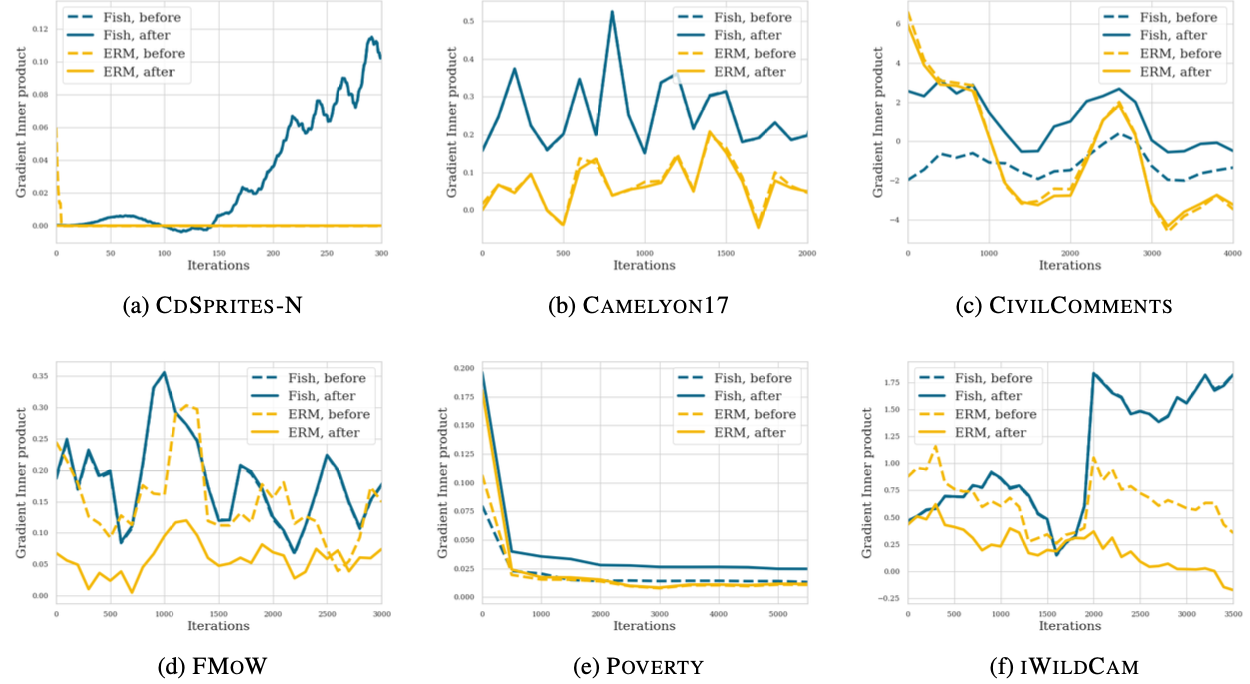GIP of the ERM and the Fish IDGM
It can be seen that there exists commonality between the training process that the GIP tends to decrease for ERM while it tends to increase or at least stay still for IDGM.
This result supports the intuition behind the proposed method that maximizing GIP can help domain generalization.