Significance
Keypoints
- Derive and propose Surrogate Gradient Field method for GAN latent space image manipulation
- Propose a metric for evaluating disentanglement of latent space manipulation methods
- Demonstrate performance of the proposed method qualitatively and quantitatively
Review
Background
Note: Background of the StyleGAN latent space manipulation methods have been overviewed in my previous post reviewing the StyleCLIP paper.
Since the discovery of the high-level disentanglement in the latent space of the StyleGAN/StyleGAN2 models, the potential use of pre-trained generators of GANs for semantic manipulation of images have been a topic of interest. The process of semantic image editing usually starts with finding the latent code of the image to manipulate. From the latent code, semantic editing is done by shifting the code to the specific direction that represents the level of a certain high-level feature. Although the latent space of the pre-trained generators are disentangled to some degree, linearly shifting the latent code often results in undesired change of other attributes. The shifting also does not provide a way to manipulate multi-dimensional information (e.g. pose), or to incorporate other general cue (e.g. text description).
The authors point out that optimizing an image classifier that takes the output of the generator to follow the latent code that satisfy the target condition can be another line of latent space manipulation method. However, training of the image classifier usually does not follow our expectation because both the pre-trained generator and the image classifier are highly non-convex neural networks, converging towards local minima due to misleading gradients. To address this issue of image classifier based latent space manipulation method, the authors train an auxiliary mapping network that induces a Surrogate Gradient Field (SGF). An algorithm is proposed to exploit this SGF network for searching the latent code of interest that satisfies the target attribute. This method has strength over previous latent space manipulation methods in that it supports multi-dimensional conditioning and incorporation of general cue.
Keypoints
Derive and propose Surrogate Gradient Field method for GAN latent space image manipulation
There are three neural network models used for the proposed method. The generator $G$ is a pre-trained StyleGAN2 (or ProGAN) generator which maps the latent code to an image $G: \mathcal{Z} \rightarrow \mathcal{X}$. The classifier $C$ predicts the semantic property $c$ of the given image $C: \mathcal{X} \rightarrow \mathcal{C}$ where the semantic property $c$ can be a vector encoding multiple semantic attributes. The auxiliary mapper $F$ is a fully-connected neural network that tries to reconstruct the latent code $z$ from a pair of the given latent code $z$ and the attribute predicted from the latent code $C(G(z))$: \begin{equation}\label{eq:aux_mapper} F(z,C(G(z))) = z. \end{equation} At first sight, the role of $F$ might be suspicious, because a function that just returns one of its inputs can perfectly satisfy the equation \eqref{eq:aux_mapper}. The role of $F$ comes when computing the gradient of $z$. But for now, we will keep the conclusion for later and start with some assumptions. Given a source image latent code $z_{0}$ and a target attribute image latent code $z_{1}$, a path $z(t), \quad t \in [0,1]$ is defined to satisfy $z(0)=z_{0}$ and $z(1)=z_{1}$.
Assumption 1. $F$ is not a trivial mapping $(z,c)\mapsto z$ which is irrespective of $c$: \begin{equation} \frac{\partial F(z, C(G(z)))}{\partial c} \neq 0 \end{equation} Assumption 2. The pre-trained $G$ is able to generate an image with the target property Assumption 3. While traversing the path, the predicted properties changes at a constant rate: \begin{equation} \frac{d C(G(z(t)))}{dt} = c_{1} - c_{0} \end{equation}
Now that the path $z(t)$ is defined, latent code $z$ can be substituted to the path $z(t)$ in the equation \eqref{eq:aux_mapper} as:
\begin{equation}
z(t) = F(z(t), C(G(z(t)))).
\end{equation}
Taking derivative on both sides with respect to $t$ results in
\begin{equation}\label{eq:sgf}
\frac{dz(t)}{dt} = (\mathbf{I} - \frac{\partial F(z(t), C(G(z(t))))}{\partial z})^{-1} \frac{\partial F(z(t), C(G(z(t))))}{\partial c} (c_{1}-c_{0}).
\end{equation}
(Full derivation is referred to the original paper.)
The r.h.s. of \eqref{eq:sgf} is called the SGF, which extends the direct linear path between the two latent codes $\frac{dz(t)}{dt}$ with a gradient field incorporating the attribute $c$.
It became clear that with the three assumptions, the auxiliary mapper $F$ takes an important role in producing a gradient field that is conditioned on $c$, guiding latent code to the target in a non-linear path.
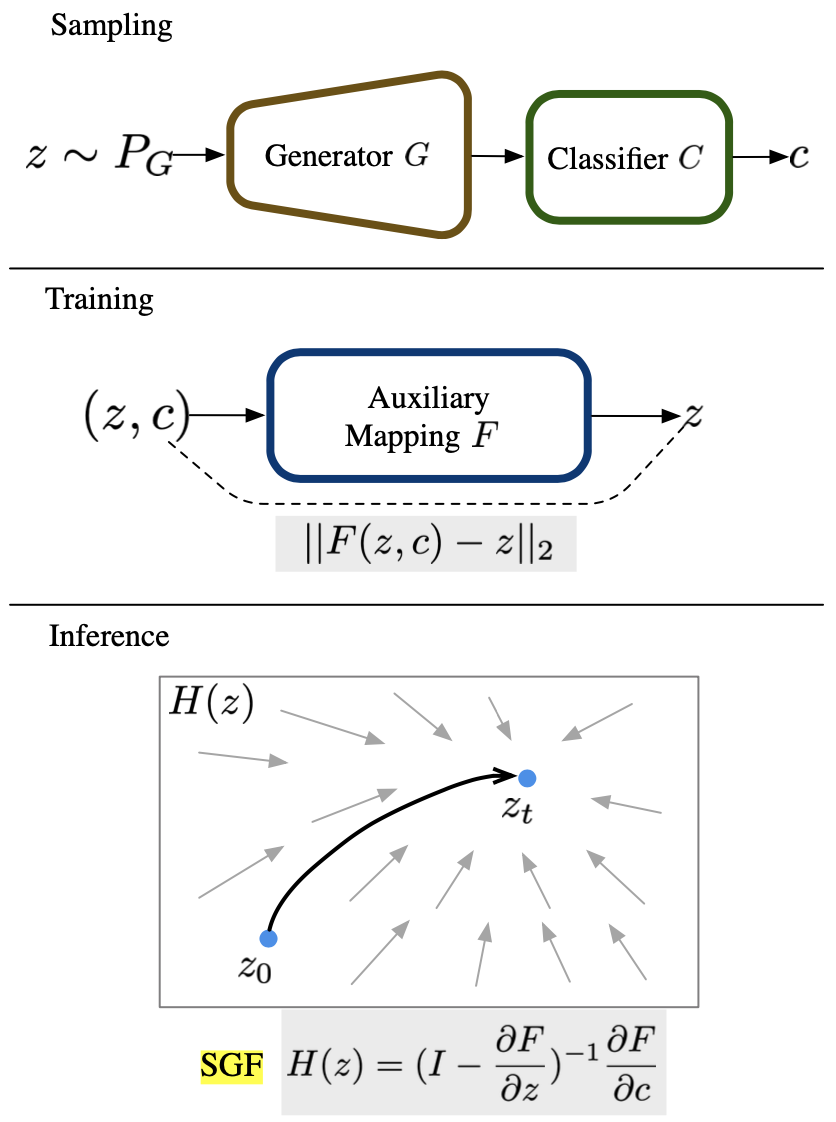Scheme of the proposed Surrogate Gradient Field method
More importantly, the authors provide a numerical solution to the proposed SGF \eqref{eq:sgf} using Neumann series expansion to approximate the matrix inversion.
Practical application of the SGF algorithm is provided in the following pseudocode, which the inner loop is the Neumann series and the outer loop is the Euler ODE solver.
Pseudocode of the proposed Surrogate Gradient Field method
Propose a metric for evaluating disentanglement of latent space manipulation methods
It remains difficult to quantitatively evaluate the level of disentanglement for latent space manipulate methods.
From the observation that a certain trade-off between the manipulation accuracy and the disentanglement exists, the authors propose to plot the Manipulation Disentanglement Curve (MDC) by gradually increasing manipulation while calculating accuracy and disentanglement.
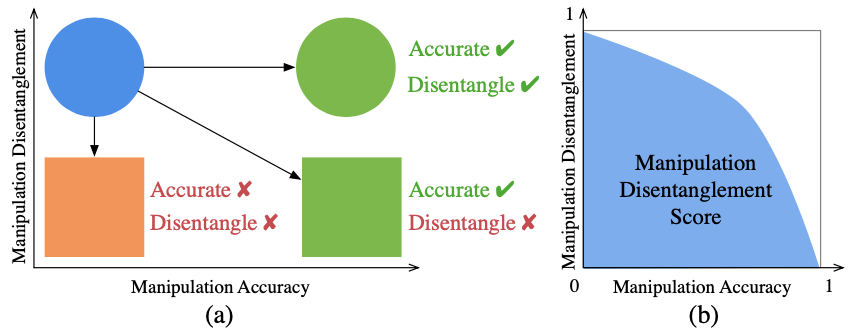(a) The trade-off of accuracy and disentanglement, (b) The Manipulation Disentanglement Curve
The quantitative metric is defined as the AUC of the MDC, named Manipulation Disentanglement Score (MDS).
Demonstrate performance of the proposed method qualitatively and quantitatively
The proposed SGF is compared with the InterFaceGAN and the GANSpace.
Quantitative results on the MDS show that the proposed method outperforms these baseline methods.
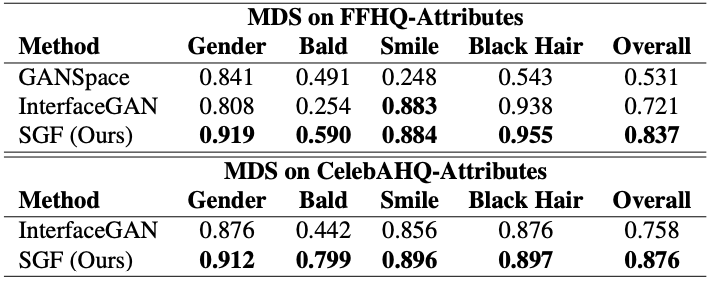Quantitative (MDS) comparison result
Qualitative results also suggest that the proposed SGF can correctly manipulate the target attribute while keeping other attributes still.
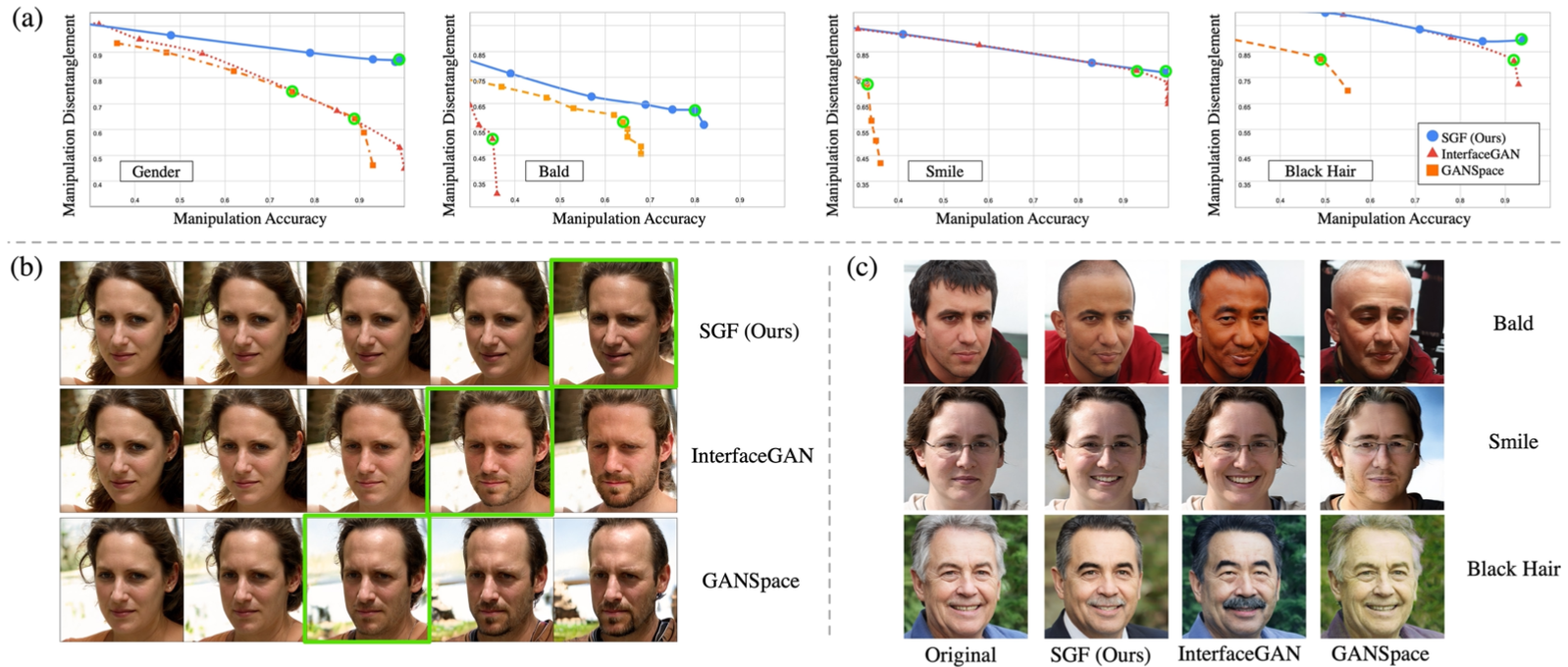Quantitative result of the SGF. (a) MDC, (b) Gender manipulation result, (c) Other attribute manipulation result.
Apart from comparison with baseline methods, the proposed method has further strength in that it supports multi-dimensional conditioning, and incorporation of the general cue.
The multi-dimensional conditioning result is provided by the facial keypoints manipulation.
Keypoints manipulation result
Incorporating the general cue for image manipulation is demonstrated with the Oxford-102 Flowers dataset which provides text description of the flower images.
Image manipulation with text result