Significance
Keypoints
- Propose a meta-learning method to fine-tune pre-trained neural networks based on non-differentiable metrics
- Demonstrate performance improvement over training with surrogate loss
Review
Background
While performance of the neural network is evaluated with the metric related to the target task (e.g. misclassification rate for image classification task), training objective is usually defined from another surrogate loss function (e.g. cross-entropy loss) because of the non-differentiability of the metric functions.
Although minimizing the surrogate loss function can indirectly guide network parameters near the global minima of the metric function space, it is still suboptimal in that the optimized network parameters are prone to hitting local bumps of the metric landscape.
The goal of this work is to propose a way to incorporate the target metric when optimizing (fine-tuning, to be specific) the neural network.
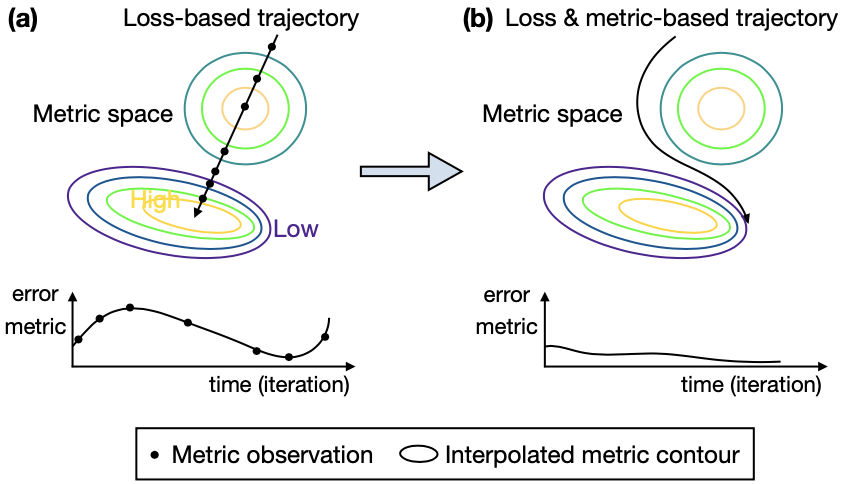(a) Surrogate loss guided optimization trajectory within metric landscape (b) Proposed metric & loss guided trajectory
Keypoints
Propose a meta-learning method to fine-tune pre-trained neural networks based on non-differentiable metrics
How can we back-propagate through a non-differentiable metric function?
The authors propose to meta-learn a differentiable multi-layer perceptron value function $f_{w_{v}}$ which maps adaptor parameters $\phi$ of the neural network $\theta$ to the metric $\mathcal{M}$,
\begin{equation}
f_{w_{v}}:\Phi \mapsto \mathcal{M}, \quad \phi \in \Phi.
\end{equation}
The name value function comes from the concept of reinforcement learning.
It can be said that the value function $f_{w_{v}}$ approximates the metric $\mathcal{M}$, and offers a way to provide supervision based on the metric when optimizing the neural network with gradient descent.
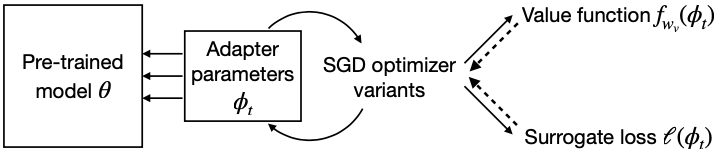Schematic illustration of the proposed method
One thing that is not clear yet is how the adapter parameters $\phi$ are defined from the full network parameters $\theta$. The authors mention that their preliminary experiments on selecting specific subsets of $\theta$, for example layer biases or last layer, did not work well. The adapter parameters are parameters from adapter modules, like conditional BatchNorm and FiLM layers. The authors define the adapter parameters $\phi$ as the FiLM parameters in the proposed method.
Now, the training of the value function $f_{w_{v}}$ is done with the following loss: \begin{align} L_{v}(w_{v}) &= \gamma L_{regress} + L_{oe}\label{eq:l_v} \\ L_{regress} &= \frac{1}{\sum^{T}_{t=1} 1 / \tilde{\sigma_{t}}} \sum\nolimits^{T}_{t=1} \frac{||f_{w_{v}}(\phi_{t})-\hat{\mathcal{M}}_{t}||_{2}}{\hat{\sigma}_{t}} \label{eq:l_regress} \\ L_{oe} &= \frac{1}{T}\sum\nolimits^{T}_{t=1}\log(1+\exp(-(D_{t,t_{n}}-D_{t,t_{p}}))), \label{eq:l_oe} \end{align} where $D_{t_{1},t_{2}} = ||g_{w_{v}}(\phi_{t_{1}}) - g_{w_{v}}(\phi_{t_{2}})||_{2}$ is the distance between the penultimate layer feature $g_{w_{v}}(\cdot)$ of the value function from inputs $t_{1}$ and $t_{2}$. The $t, t_{p}, t_{n}$ are elements of the timepoints ${1,…,T}$ serving as anchor, positive sample, and negative sample, respectively. The positive and negative samples are defined with respect to the anchor based on how much the metrics can be discriminated by the Fisher’s ratio. Although the details of the positive/negative sampling are referred to the original paper, it is clear from \eqref{eq:l_oe} that the sampling is required for the ordinal embedding loss $L_{oe}$. As it can be seen in \eqref{eq:l_v}, the ordinal embedding loss $L_{oe}$ provides regularization in feature space weighted by $\gamma$ when optimizing the main regression objective \eqref{eq:l_regress} between the value function and the metric.
Important intuitions of the proposed method, Metric Optimizer (MetricOpt), are discussed by far and some practical solutions for training and testing are left.
To be short, the Reptile algorithm and the Guided ES approach are applied for meta-training and -testing the MetricOpt.
Pseudocode of the proposed MetricOpt
Demonstrate performance improvement over training with surrogate loss
The performance improvement is first experimented with ResNet-32 on CIFAR-10 dataset. The training or optimization means fine-tuning of the pre-trained ResNet model in the experiments.
It could be seen that the non-differentiable metric AUCPR is stably minimized throughout the training steps with the proposed MetricOpt methods.
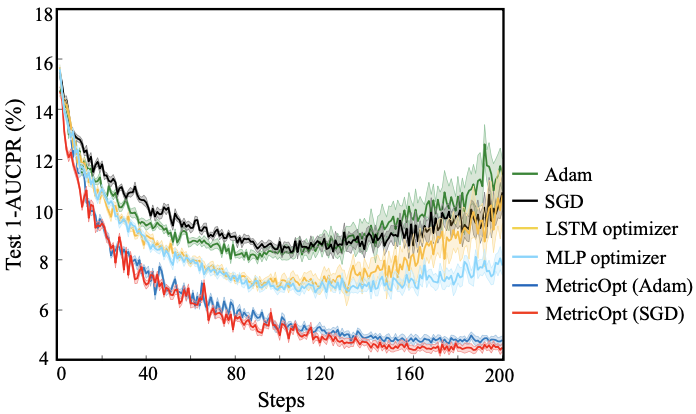Training progress of different optimization methods
The final misclassification rate (MCR) and AUCPR was also better when optimizing with MetricOpt methods and the surrogate loss.
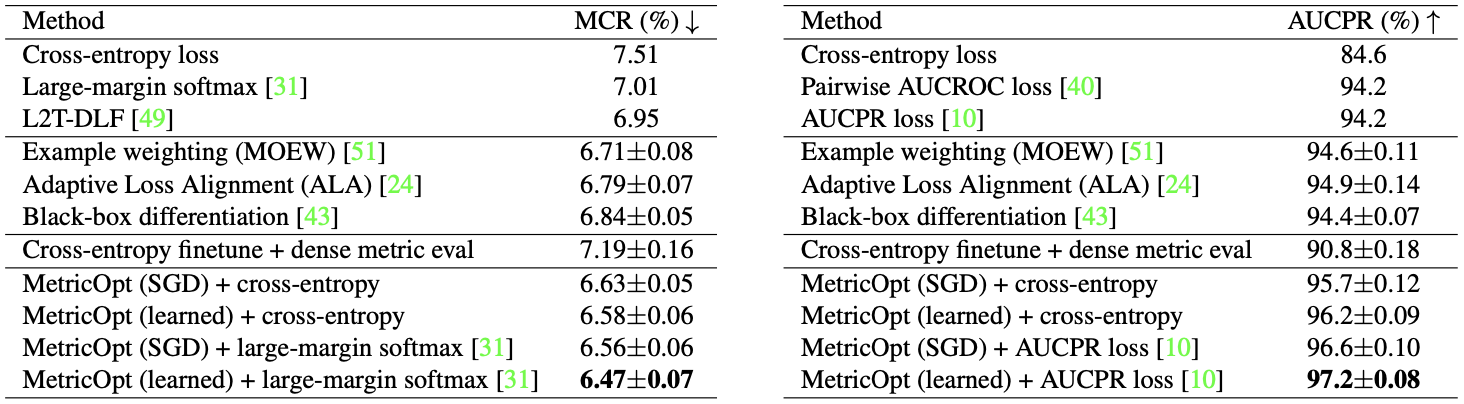Quantitative performance of the MetricOpt
It should be noted that the MetricOpt algorithm reviewed in previous subsection refers to MetricOpt(SGD) in the Table.
See supplementary B of the original paper for description on the MetricOpt(learned).
Experiments on other settings provide evidence that the MetricOpt can (i) work well on other tasks such as image retrieval and object detection,
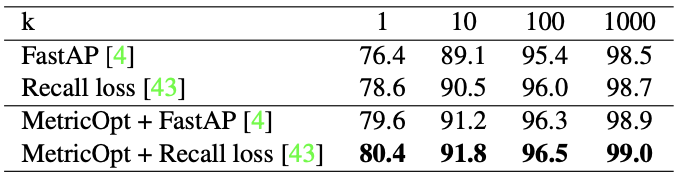Image retrieval on Stanford Online Products dataset
Object detection on Pascal VOC 2007 dataset
(ii) improve performance for non-image data,
Binary classification on A9A, CoverType (Cov) datasets
and (iii) generalize to other model architectures and datasets.
Image classification on ImageNet dataset with NASNet-A model