Significance
Keypoints
- Propose self-attention layer with pooling function for hierarchical multiscale video/image recognition
- Demonstrate performance and computational efficiency of the proposed method by experiments
Review
Background
Vision Transformers (ViTs) are starting to replace the convolution neural networks (CNNs) in many computer vision tasks, as the Transformers have replaced the recurrent neural networks (RNNs) in most of the natural language processing tasks. However, CNNs still have their architectural strengths in solving computer-vision tasks which ViTs do not. For example, CNNs inherit locality from the convolution operation, which is important for handling image data (since images tend to hold locally-similar property). Another architectural point of the CNNs is that pooling layers within the network can provide computational efficiency and hierarchical higher-level feature learning at the upper layers. While some recent ViT models tried to address the locality issue (see my previous post on ConViT and LocalViT), this work focuses on bringing the pooling layers to improve the ViTs.
Keypoints
Propose self-attention layer with pooling function for hierarchical multiscale video/image recognition
Multi Head Pooling Attention (MHPA)
The authors propose Multi Head Pooling Attention (MHPA), which uses pooling operator to reduce the space-time resolution of the mapped query, key, and value embeddings.
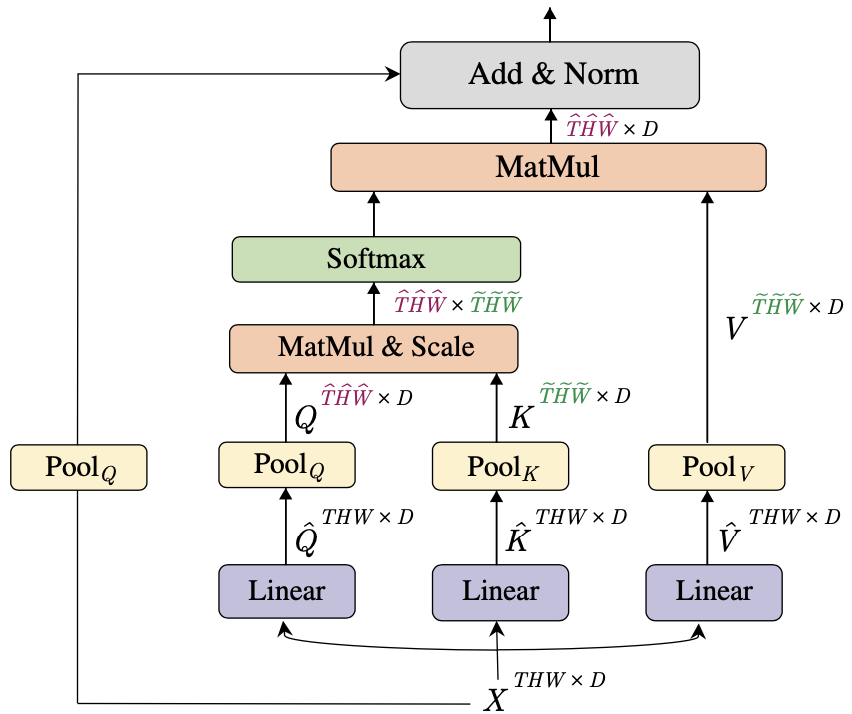Proposed Multi Head Pooling Attention (MHPA) layer
The cornerstone part of the MHPA is the pooling operator $\mathcal{P}(\cdot ; (\mathbf{k},\mathbf{s},\mathbf{p}))$, which performs a pooling kernel computation with kernel $\mathbf{k}$, stride $\mathbf{s}$, padding $\mathbf{p}$ parameters with shapes of $k_{T} \times k_{H} \times s_{W}$, $s_{T} \times s_{H} \times p_{W}$, $p_{T} \times p_{H} \times k_{W}$, respectively.
Let length $L=T \times H \times W$, then the reduced length after pooling operator is given by:
\begin{equation}
\tilde{L} = \left\lfloor\frac{L+2\mathbf{p}-\mathbf{k}}{\mathbf{s}}\right\rfloor + 1. \notag
\end{equation}
In short, the pooling operator is a mapping $\mathcal{P}:\mathbb{R}^{L \times D}\mapsto \mathbb{R}^{\tilde{L}\times D}$, where $D$ is the channel dimension of each embedding.
The default setting in this paper uses overlapping kernels and shape preserving padding, so the overall reduction of the length is dependent on only the stride $\mathbf{s}$.
Apart from the pooling operator, the computation of the MHPA is almost identical to the original self-attention layer of the ViT so is not reviewed here.
Multiscale Vision Transformer (MViT)
A scale stage is a set of MHPA layers that operate on the same scale (i.e. same length $L$ and same channel dimension $D$).
The proposed model Multiscale Vision Transformer (MViT) consists of multiple scale stages, with stage transition which reduces the length $L$ while increasing the channel $D$ between the stages.
Structure of the MViT
This structure of increasing channels and decreasing resolution can be said to follow typical composition of the convolution layers in CNNs, bringing hierarchical multiscale processing capability to the ViT.
Demonstrate performance and computational efficiency of the proposed method by experiments
Video recognition
The performance of the MViT is compared to other models including X3D, SlowFast, ViViT, TimeSformer, and VTN for video recognition task using Kinetics-400 (K400) and Kinetics-600 datasets.
One of the major strength of the MViT over conventional ViT is the computational efficiency.
Since the spatial resolution is related to the number of required computation with a factor of two, reducing the spatial resolution by half can lead to four times increased efficiency.
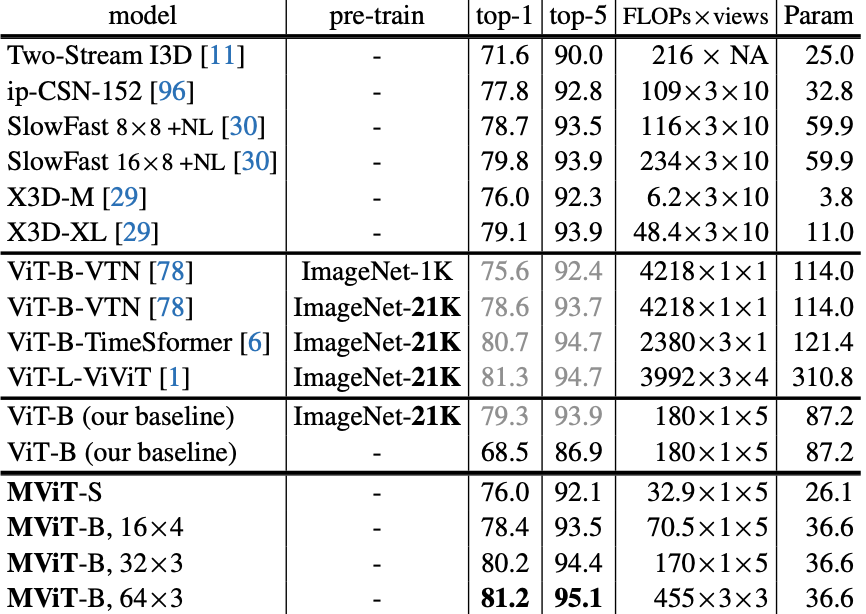Performance comparison of MViT for K400 dataset
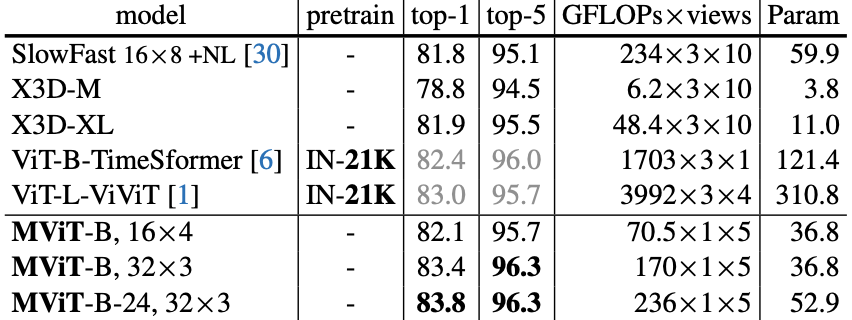Performance comparison of MViT for K600 dataset
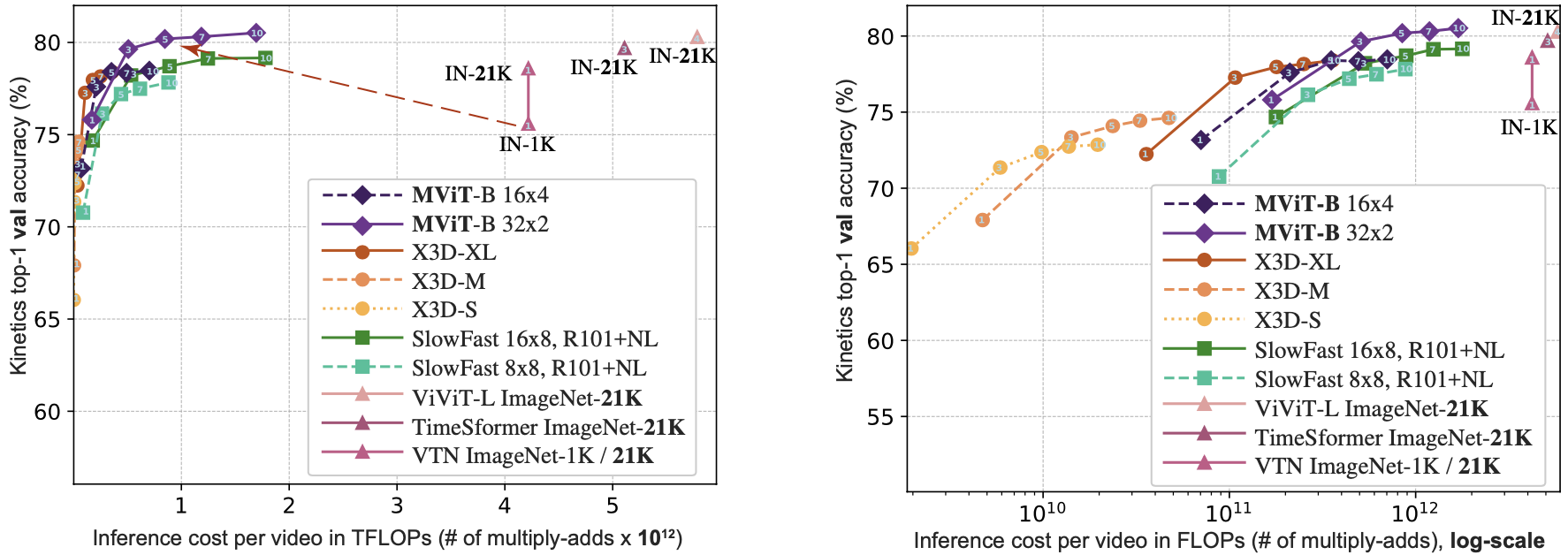Accuracy with respect to computational cost in the K400 validation set
It should be noted that the training of MViT did not require pre-training with an external dataset.
The authors test whether the model takes the temporal information into account by performance drop after random shuffling of the video frames.
Interestingly, the MViT showed significant reduction in the classification accuracy indicating the temporal information is important for the model, while the ViT did not show apparent decline in the performance.
Frame shuffling study result
Other experiment results including ablation studies and transfer learning performance on Something-something-v2, Charades, and AVA datasets are referred to the original paper.
Image recognition
The image recognition task can be thought of a video recognition task with a single frame, $T=1$.
Experiments are carried out on the ImageNet-1K dataset, and showed comparable performance to other models including the EfficientNet and the DeiT.
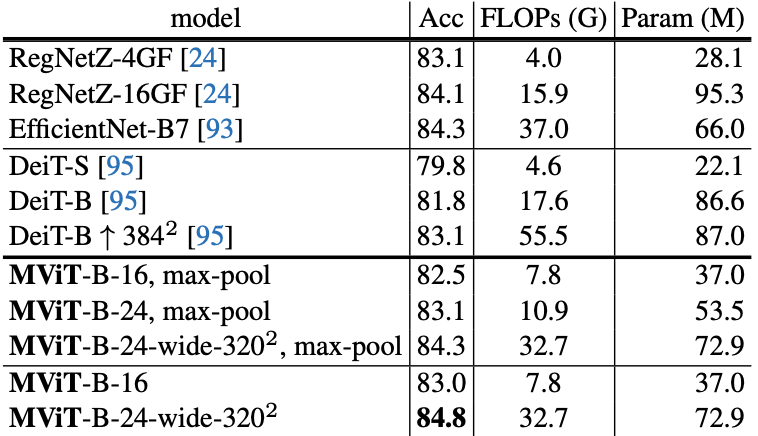Performance comparison of MViT for ImageNet dataset