Significance
Keypoints
- Propose a sparse backpropagation method for spiking neural networks
- Demonstrate efficency and performance of the proposed method by experiments
Review
Background
Spiking neural networks (SNNs) are neural networks with $N^{(l)}$ neurons at each layer $l$, fully connected to the next layer through synaptic weights $W^{(l)}\in \mathbb{R}^{N^{(l)}\times N^{(l)+1}}$. Each neuron has an internal state variable $V_{j}^{(l)}[t] \in \mathbb{R}$ being updated at each timestep $t$. A spike $S_{i}^{(l)}[t]$ is emitted by a neuron at time $t$ based on the internal state $V_{i}^{(l)}[t]$ and the spiking function $f: \mathbb{R} \rightarrow \{0,1\}$ such that \begin{align} S_{i}^{(l)}[t] = f(V_{i}^{(l)}[t]). \end{align} The spiking function is commonly defined as a unit step function with threshold $V_{th}$: \begin{align}\label{eq:spiking} f = \begin{cases}1,\quad,v>V_{th} \\ 0,\quad \mathrm{otherwise}\end{cases} \end{align}
One of the discretized forward-pass model of the SNN is given by the \begin{align}\label{eq:forward} V_{j}^{(l)}[t+1] = -\alpha (V_{j}^{(l+1)}[t] - V_{rest}) + \sum_{i} S_{i}^{(l)}[t]W_{ij}^{(l)} - (V_{th} - V_{r})S_{j}^{(l+1)}[t], \end{align} where $V_{r}$ is the reset potential (the value a neuron is reset to after spiking). The first term of \eqref{eq:forward} accounts for the leakage of potential as the time passes, while the second term stands for the integration of spikes. The last term is the resetting term. Setting the values $V_{rest} = 0$, $V_{th} = 1$, $V_{r} = 0$, and $V_{i}^{(l)} = 0 \forall l, i$, the forward-pass \eqref{eq:forward} can be reformulated into: \begin{align} V_{j}^{(l+1)} [t+1] = \sum^{t}_{k=0}\alpha^{t-k}S_{i}^{(l)}[k]W_{ij}^{(l)} - \sum^{t}_{k=0}\alpha^{t-k} S_{j}^{(l+1)}[k]. \end{align} The spiking function $f$ being a unit step function \eqref{eq:spiking}, it is easy to compute the forward-pass, while it is not the case for the backward-pass gradients.
Keypoints
Propose a sparse backpropagation method for spiking neural networks
To backpropagate through the SNN, the gradient of the loss function with respect to the weights in each layer: \begin{align} \nabla W_{ij}^{(l)} = \sum_{t} \epsilon _{j}^{(l+1)}[t] \frac{dS_{j}^{(l+1)}[t]}{dV_{j}^{(l+1)}[t]} \Bigl(\sum_{k<t}\alpha^{t-k-1}S_{i}^{(l)}[t] \Bigr) \end{align} should be tractable, where $\epsilon$ refers to the gradient from the next layer, i.e. $\epsilon_{j}{(L-1)}[t]$ is the gradient of the loss w.r.t the final layer and $\epsilon_{j}{(l)}[t] = \nabla S_{j}^{(l)}[t]$. The expression for $\epsilon_{i}^{(l)}[t]$, or $\nabla S_{i}^{(l)}[t]$, as a function of the next layer gradietn $\nabla S_{i}^{(l+1)}[t]$ can be obtained by \begin{align} \epsilon_{i}^{(l)}[t] &= \nabla S_{i}^{(l)}[t]= \sum_{j} W_{ij} \Bigl( \sum_{k>t} \nabla S_{j}^{(l+1)}[t] \frac{dS_{j}^{(l+1)}[t]}{dV_{j}^{(l+1)}[t]} \alpha^{k-t-1} \Bigr) \\ &= \sum_{j} W_{ij} \delta_{j}^{(l+1)}[t],\quad l=\{0,1,…,L-2 \}. \end{align}
To make the backpropagation sparse, the authors define a neuron $j$ to be active if $|V_{j}[t] - V_{th}|<B_{th}$ for a certain bound $B_{th}$, which means that the potential of the neuron is close to the threshold at a certain level. Now, the spike gradient is defined as: \begin{align} \label{eq:spike_grad} \frac{d_{j}[t]}{dV_{j}[t]} := \begin{cases}g(V_{j}[t]),\quad \text{if} V_{j}[t] \text{is active} \\ 0, \quad \mathrm{otherwise}, \end{cases} \end{align} where $g(V) := 1 / (\beta |V - V_{th}| 1)^{2}$ is the surrogate gradient. This new definition of the spike gradient ensures the backprogation to be sparse (by letting only the active neurons backpropgate), and to be differentiable by $g$.
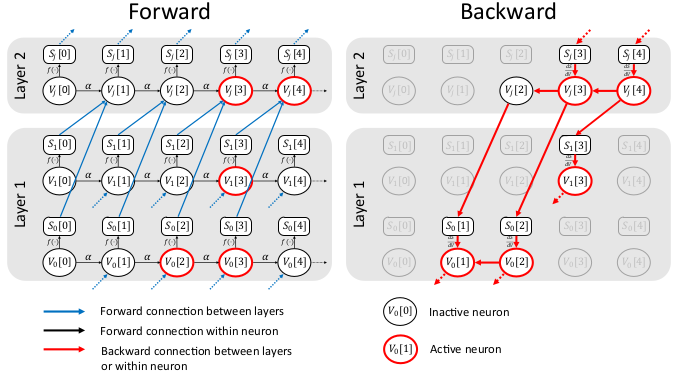Schematic illustration of the proposed sparse backpropagation
The final definition of sparse gradient becomes: \begin{align} S_{j}^{(l)}[t] = \begin{cases} W_{ij} \delta_{j}^{(l+1)}[t],\quad \text{if} V_{j}[t] \text{is active} \\ 0, \quad \mathrm{otherwise}. \end{cases} \end{align} where the derivation from \eqref{eq:spike_grad} is referred to the original paper.
Demonstrate efficency and performance of the proposed method by experiments
The experiments are performed on a three-layer SNN with 200 neurons. Fashion-MNIST, Neuromorphic-MNIST, and Spiking Heidelberg Dataset (SHD) were used as the benchmark datasets.
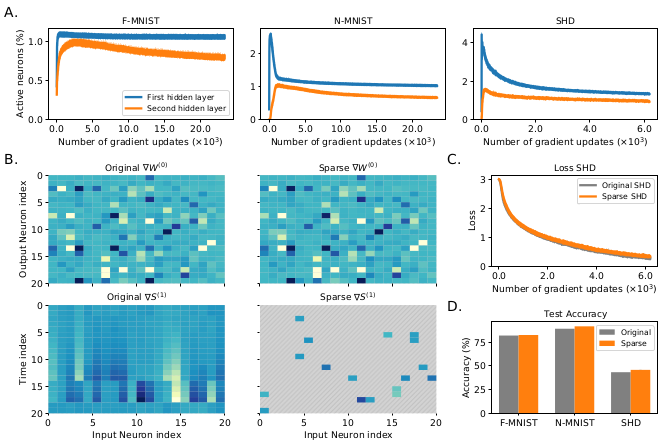Experimental results of the proposed method regarding (a) sparsity (b) similarity to dense backpropagation (c) loss curve (d) performance
According to (a) of the above figure, the active neurons stay around 0.5~5.0\% of the total neurons during training.
Despite the sparsity, the gradient of the sparse backpropagation show a similar pattern to that of the original dense gradient as seen in (b) of the above figure, which suggests that the proposed sparse backpropagation approximates the original gradient well.
The classification accuracy of the proposed method achieves at least comparable performance to the original backpropagation, as can be seen in (d) of the above figure.
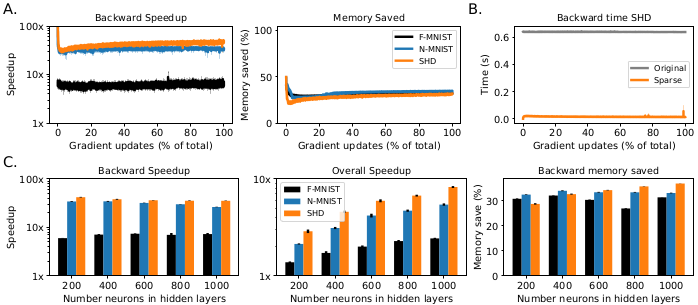Memory save and speedup of the proposed method
As expected, the proposed sparse backpropagation is more memory efficient and achieves faster speed ((a) of the above figure).
The time taken for backpropagation is significantly reduced from the original case around 640ms to around 17ms (b).
This memory efficiency and speedup is robust with respect to the increased number of neurons in the hidden layers (c).
The authors comment that the proposed sparse backpropagation algorithm on SNNs could open a possibility for fast and energy efficient end-to-end on-chip training in the future.