Significance
Keypoints
- Propose two adversarial robustness measures based on flatness of loss landscape
- Show relationship between the flatness and the robust generalization gap by experiments
Review
Background
Generalization of a trained deep neural network is still a mysterious phenomenon. The neural network learns to properly make prediction over unseen dataset, but it is not yet clear where this capability emerges from. Ideas that try to explicitly measure generalization gap (the gap between the training and the test performance) are being studied, incorporating mathematical ideas to evaluate distance (norm), sharpness/flatness, margin, or output sensitivity, but no single measure has been proved to work well at all conditions (there even was a competition at the NeurIPS 2020 for predicting the genralization gap).
Adversarial training is a widely adopted technique when training a neural network for improving adversarial robustness and test-time performance. More formally, a small perturbation $\delta$ is added to the input data $x$ when training the neural network $f$ with weights $w$: \begin{equation} \min_{w}\mathbb{E}_{x,y}[ \max_{||\delta||_{p \leq \epsilon}} \mathcal{L}(f(x+\delta ; w),y) ], \end{equation} where $\epsilon$ is a prespecified perturbation upper-bound, and $y$ is the corresponding label. However, robust overfitting is found to be a common problem in adversarial training. A recent work suggests that the flatness of the weight loss landscape is related to the robust generalization gap, but the paper has investigated this relationship by qualitatively by visualizing the loss landscape with respect to a random perturbation. The authors address this issue and propose a quantitative robustness measures based on flatness of the loss landscape which is scale-invariant, enabling comparison across different models. Relationship between the flatness and the robust generalization gap is evaluated using the proposed measures.
Keypoints
Propose two adversarial robustness measures based on flatness of loss landscape
The flatness of the loss landscape can be visualized (i.e. qualitatively measured) by perturbing the weight in a random direction and measuring the difference of the loss caused by the perturbation.
The authors propose two objective flatness measures, the average-case and the worst-case flatness, where average-case flatness is defined as:
\begin{equation}\label{eq:avg_flatness}
\mathbb{E}_{\nu} [ \underset{||\delta||_{\infty}\leq \epsilon}{\max} \mathcal{L}(f(x+\delta ; w + \nu), y)] - \underset{||\delta||_{\infty}\leq \epsilon}{\max} \mathcal{L}(f(x+\delta ; w ), y),
\end{equation}
where $\nu$ is the random weight perturbation.
The second term of the \eqref{eq:avg_flatness} is the reference term that the authors propose to make the measure independent of the absolute loss.
Losses $\mathcal{L}$ and the $\tilde{\mathcal{L}}$ represent the second and first term of \eqref{eq:avg_flatness}, respectively
For the worst-case flatness, the expectation over the left term is substituted with the maximum value with respect to the $\nu$.
Show relationship between the flatness and the robust generalization gap by experiments
The authors provide relationship between the flatness and the robust generalization from a variety of perspectives.
First, the relationship between the robust generalization and the flatness is plotted with the proposed measure \eqref{eq:avg_flatness} to find correlation between the two.
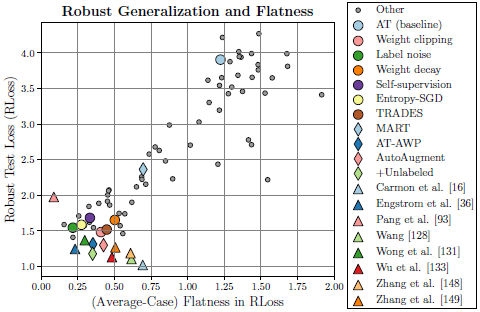Robust generalization correlates with flatness
Flatness throughout the adversarial training, flatness across hyper-parameters, and the effect of early stopping in robust generalization along with flatness are demonstrated.
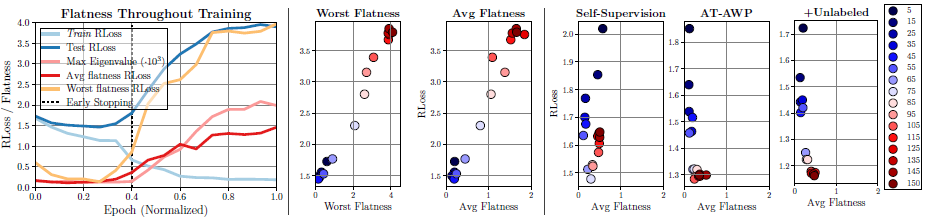Flatness throughout training
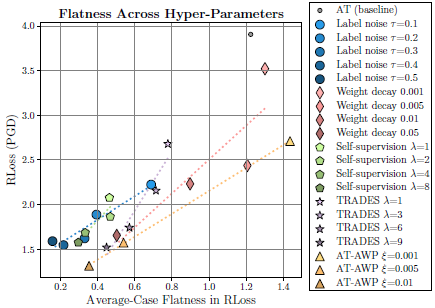Flatness across hyper-parameters
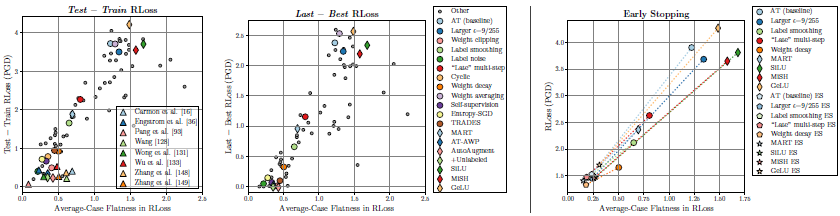Flatness and early stopping
The authors conclude that the provided measures allow comparison between the models, and consistently finds correlation between the loss landscape flatness and the robust generalization gap in extensive experiments.