Significance
Keypoints
- Propose a saliency mapping method that is grounded on the information theory
- Demonstrate qualitative and quantitative performance of the proposed method
Review
Background
Explainability in artificial intelligence is an important topic in the fields where the reasons for the model’s decision are of interest (e.g. medicine). One of the major streams of the explainability method is the back-propagation based method. The back-propagation based methods exploit the fact that back-propagation computes derivative of the input with respect to the prediction, which can be seen as how much the prediction is sensitive to the input. However, recent studies suggest that these methods may not faithfully represent the model’s decision process. To address this issue, the authors propose Mutual Information Preserving Inverse Network (MIP-IN), a saliency mapping method that is grounded on the information theory (but not very much related to back-propagation if I understood correctly…).
Keypoints
Propose a saliency mapping method that is grounded on the information theory
Problem formulation
The key idea of the proposed method comes from an intuitive idea that the mutual information between the input variable $X$ and the prediction output variable $Y$ from a trained model $\Phi$ should be high, in order to faithfully visualize the decision made from the model. The aim is to learn a set of source signal $S=\{s\}$ and distractor signal $D=\{d\}$ that compose the input $x=s+d$. Here, the source signal is the input signal which is relevant to the decision-making of the model, whereas the distractor signal is not. Now, it is straightforward that the mutual information between the source signal $S$ and the prediction $Y$ should be high, suggesting the following optimization problem of $S$: \begin{equation}\label{eq:min_s} \min_{S} | I(X;S) - I(X;Y) |. \end{equation} Our goal is to estimate $S$ from prediction $Y$ with a learnable function $g$ which satisfies \eqref{eq:min_s}. Since the mutual information $I(X;Y)$ is constant for a trained model $\Phi$, and from the data processing inequality $I(X;S) \leq I(X;Y)$, the optimization problem \eqref{eq:min_s} can be reformulated as: \begin{equation} \label{eq:max_g} \max_{g} I(X, g(Y)) = H(X) - H(X|g(Y)). \end{equation} Considering that the entropy of input $H(X)$ is constant, the optimization in \eqref{eq:max_g} is equivalent to minimizing the conditional entropy $H(X|g(Y))$. To overcome the intractability of $H(X|g(Y))$, the authors bring Fano’s inequality to derive that minimizing the reconstruction error between the $X$ and the $g(Y)$ corresponds to minimizing the upper bound of the conditional entropy of interest $H(X|g(Y))$. So, the problem is simplified to solving \begin{equation}\label{eq:min_g} \min_{g}|X-g(Y)| \end{equation} with a learnable function $g$.
For further information on important inequalities of the information theory, see chapter 2 of Cover and Thomas, 2006.
MIP-IN: Mutual Information Preserving Inverse Network
The $g$ is a neural network with the same number of layers as the pre-trained model of interest $\Phi$. The authors propose to optimize \eqref{eq:min_g} by minimizing the signal $S_{l+1}$ and the feature $X_{l}$ at every layer $l$: $\min_{g_{l+1}}||X_{l} - g_{l+1}(S_{l+1})||^{2}$. One important problem here is that the trained $g$ can only account for the average across the prediction output variable $Y$, while our interest is in source signal $s$ of a specific sample $x \in X$. To introduce locality, the authors propose to apply following indicator function to the $S_{l}$ based on whether the ReLU activation of the neuron $i$ was positive or zero at the feed-forward step: \begin{equation} \text{Indication}(i) = \begin{cases} 1 \quad \text{if } X_{l}(i) \neq 0, \\ 0 \quad \text{if } X_{l}(i) = 0 \end{cases} \end{equation} The authors mention that the intuition behind this indicator function is based on the continuity assumption, which I did not understand yet. By masking the signal at layer $l$ with the indicator function as $S_{l} = S_{l}\bigodot \text{Indication}$, sample specific source signal $s$ can now be obtained.
The layers of $g$ can be one of fully-connected, convolution, or the max-pool.
Attribution $A$ is the superposition of attribution $A_{l}$ at layer $l$ which is defined as the weight of the MIP-IN model $g_{l+1}$ at layer $l+1$.
Pseudocode of the MIP-IN
It can be seen from the result that the global signal does not follow to explain decision based on each samples, while the local signal represents the decision from each samples.
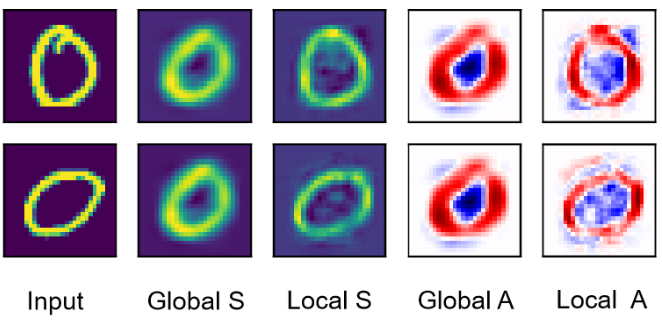Global/local source signal $S$ and attribution $A$
Demonstrate qualitative and quantitative performance of the proposed method
For the experiments, a three layer MLP was used for the MNIST dataset and pre-trained VGG19 or Resnet50 was used for the ImageNet dataset. The MIP-IN is trained after the model (MLP, VGG19, or Resnet50) was frozen, which is reported to take less than a minute. In practice, only the upper layers are trained and used for saliency mapping (by resizing the upper layer saliency map similar to the Grad-CAM)
The performance of the MIP-IN is first shown qualitatively by exemplar visualization of the saliency map.
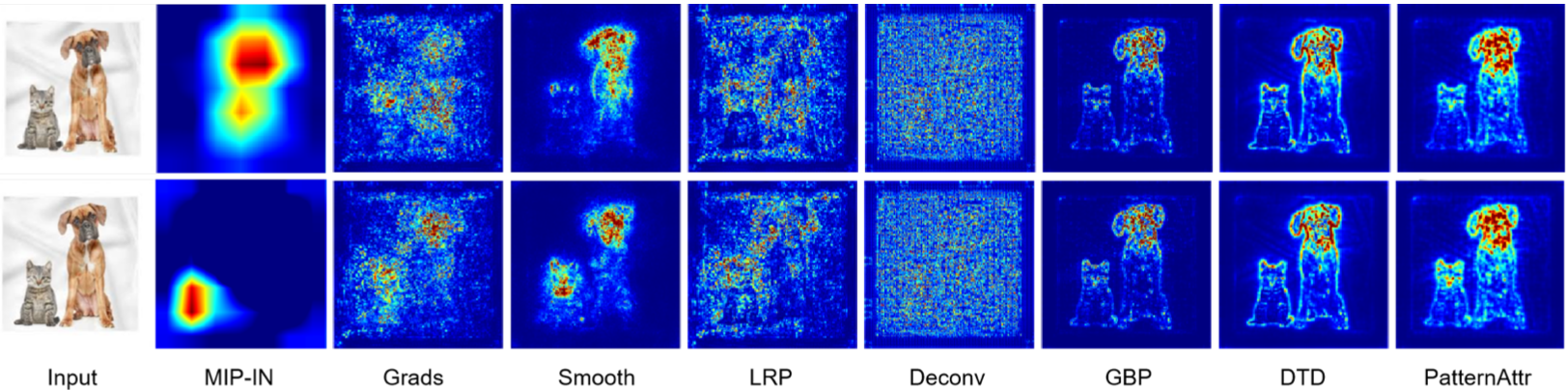MIP-IN provides better visualization without noisy background
For quantitative evaluation, the localization performance was computed by the accuracy of the saliency map with the provided bounding box labels.
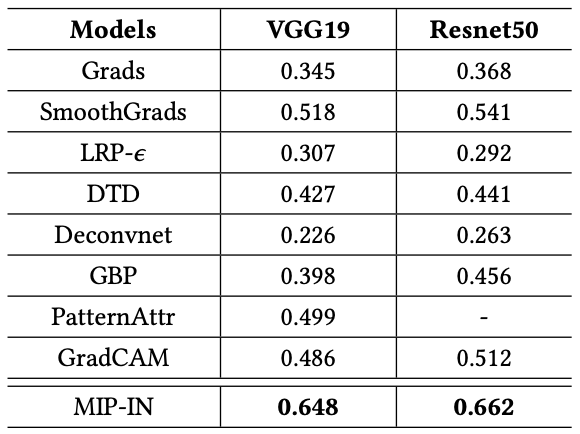Bounding box match accuracy
Lastly, the authors evaluate class label sensitivity, considering that there are issues with the back-propagation based saliency mapping methods can generate explanations that are not sensitive to the change in class labels.
The class label sensitivity is computed by selecting two random classes and computing the average L2 distance between the saliency maps inferred from the two classes.
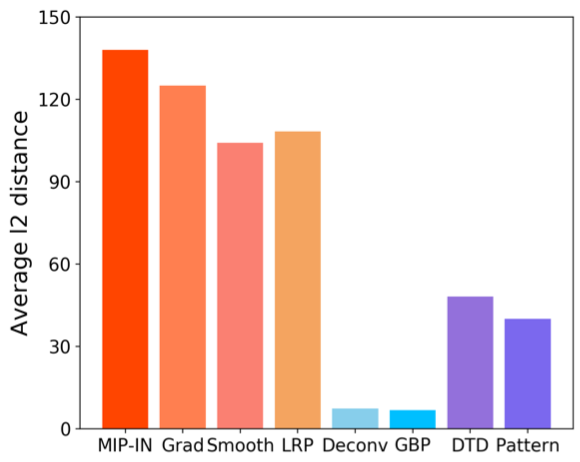MIP-IN shows better class label sensitivity
This paper proposes an interesting explainability method based on the information theory. The derivation of the theoretical background is quite precise and straightforward. However, the need for separately training the model (MIP-IN) for saliency mapping might be a small limitation of the proposed method. And I wouldn’t say that the MIP-IN is related to back-propagation from any perspective because the explainability comes from the forward pass of the newly trained $g$. It seems that the MIP-IN is mostly related to the information theoretical perspective.