Significance
Keypoints
- Propose an adversarial training scheme for out-of-manifold regularization of text classification models
- Demonstrate text classification performance of the proposed method by experiments
Review
Background
Many natural language processing (NLP) tasks, including text classification, have enjoyed huge success since the introduction of self-attention based models (Transformer) and application of self-supervised training schemes (BERT). The self-supervised training allowed a stack of Transformer encoders to be pre-trained with a large corpus of unlabelled text data, which learns to extract meaningful vector representation of each input tokens. However, current training objective focuses on learning the in-distribution representation of the text corpus, leading to inefficient embedding in the high-dimensional latent space. The authors address this issue, and propose an adversarial training objective to regularize out-of-manifold (OOM) distribution.
Keypoints
Propose an adversarial training scheme for out-of-manifold regularization of text classification models
The idea is to adversarially train a generator $G$ and a discriminator $D$ which generates OOM samples, and discriminates whether the input is from OOM or in-distribution.
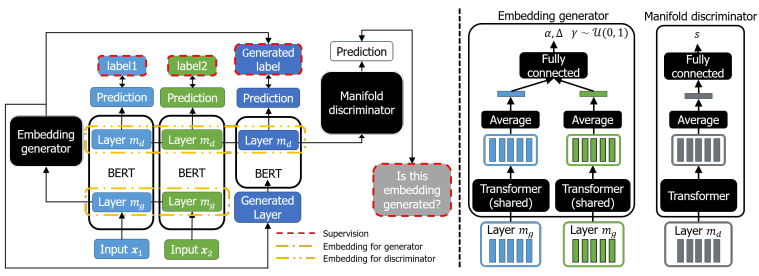Schematic illustration of the proposed method
The generator takes two latent embeddings $\mathbf{h}_{1}^{m_{g}}$ and $\mathbf{h}_{2}^{m_{g}}$ to output a OOM sample by linear interpolation of the two vectors with coefficient $\lambda$:
\begin{align}
G(\mathbf{h}_{1}^{m_{g}},\mathbf{h}_{2}^{m_{g}}) &= \lambda \cdot \mathbf{h}_{1}^{m_{g}} + (1-\lambda ) \cdot \mathbf{h}_{2}^{m_{g}} \\ \lambda &= \alpha + \gamma \times \Delta,
\end{align}
where $\alpha$, $\Delta$ are inferred by applying two-layer MLP to the concatenated sentence-level embeddings, and $\gamma \approx \mathcal{U}(0,1)$ (see ‘Embedding generator’ part of the above figure).
However, the authors mention that training with only the generator $G$ result in the model to memorize the data seen during training.
To generate novel embeddings from the generator, the discriminator $D$ takes sentence-level embedding obtained by averaging the whole embeddings of layer $m_{g}$ including the generated one (see ‘Manifold discriminator’ part of the above figure).
Discriminator then outputs a scalar value in $[0,1]$ to predict whether the embedding includes fake or not.
The final objective for training is defined by:
\begin{equation}
\underset{(\mathbf{x},y)\approx D}{\mathbb{E}}[\mathcal{L}_{C}(\mathbf{x},y)+ \mathcal{L}_{G}(\mathbf{x},y)+ e\mathcal{L}_{D}(\mathbf{x})]
\end{equation}
where $e$ is the discriminator coefficient and $\mathcal{L}_{C}$, $\mathcal{L}_{G}$, $\mathcal{L}_{D}$ indicates classification, generator, discriminator loss, respectively.
Demonstrate text classification performance of the proposed method by experiments
The proposed method, OoMMix is experimented on four benchmark sentence classification datasets, AG News, Amazon Review, Yahoo Answer, and DBpedia.
Baseline models include existing mixup approaches, such as NonlinearMix, mixup-transformer, TMix, and MixText.
The results indicate that OoMMix outperforms other mixup techniques and the baseline model
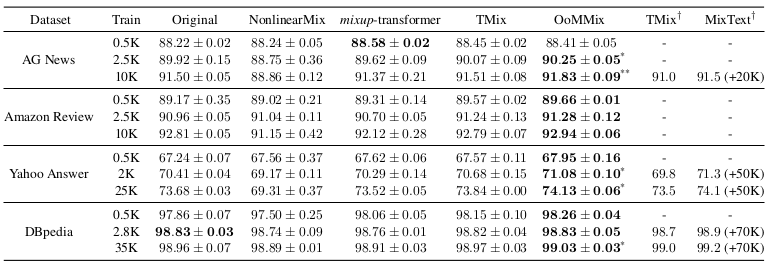Quantiative performance of the proposed method
The performance gain was also apparent when data augmentation techniques including EDA, BT, and SSMBA are applied.
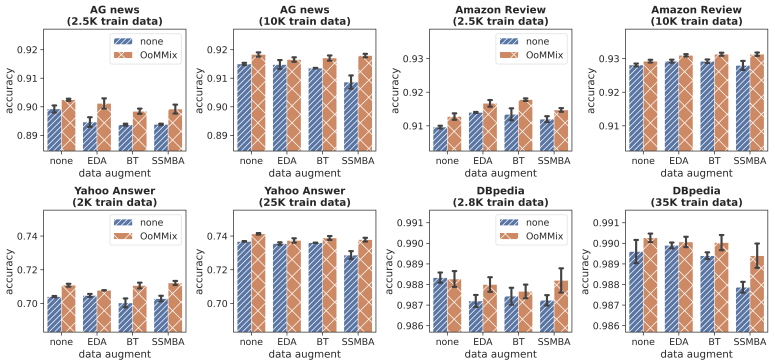Compatibility of OoMMix with data augmentation
To investigate the effect of the manifold discriminator, the histogram of mixing coefficients is plotted with respect to the presenced of the discriminator $D$.
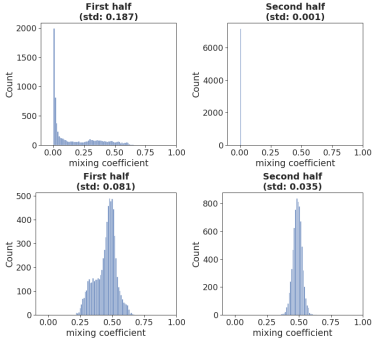Mixing coefficient without (upper) and with $D$ (lower)
Further evaluation of the proposed model, including the effect of different embedding layers and the manifold visualization are referred to the original paper.