Significance
Keypoints
- Propose a framework for generalizing GNNs to HyperGNNs
- Demonstrate performance of UniGNN for hypernode classification tasks
Review
Background
A graph $G=(V,E)$ is defined as a pair of a vertex set $V$ and an edge set $E$, where the edge set again contains a pair of vertices that have connection.
A hypergraph $H=(V,\mathcal{E})$ is an extension of the graph, that the elements in hyperedge set $\mathcal{E}$ need not be a pair but can be any subset of $G$ (except $\emptyset$).
This means that an edge of a hypergraph can connect more than two vertices at once.
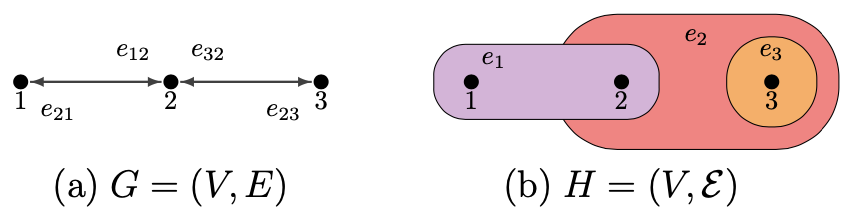Example of a (a) Graph, and a (b) Hypergraph
Along with the success of the Graph neural networks (GNNs), interest in learning representation of hypergraphs with a neural network has increased. Although attempts have been made to bring the power of the GNNs into hypergraph neural networks(HyperGNNs), direct extension of powerful GNN structures into hypergraphs have not yet been available. The goal of this paper is to propose a framework that directly extends the design of well-known GNNs into HyperGNNs while addressing the key questions from the GNNs: over-smoothing problem and the discriminative power.
Keypoints
Propose a framework for generalizing GNNs to HyperGNNs
GNNs learn to extract representation of vertices by the message-passing scheme:
\begin{equation}\label{eq:mp}
\text{(GNN)} x^{l+1}_{i} = \phi^{l}(x^{l}_{i}, \{ x^{l}_{j} \} _{j\in\mathcal{N}_{i}}),
\end{equation}
where $x^{l}_{i}$ is the feature vector of node $i$ at layer $l$, $\mathcal{N}_{i}$ is the neighborhood of node $x_{i}$, and $\phi$ is the message-passing function.
The message-passing scheme \eqref{eq:mp} can be separated into two steps:
\begin{equation}\label{eq:mp_twostep}
\text{(GNN)} \begin{cases} h_{e} = \phi_{1} (\{ x_{j} \} _{j \in e}), \\ x_{i} = \phi_{2} (x_{i}, h_{e}), \end{cases}
\end{equation}
where $\phi_{1}$ can be thought of AGGREGATE function that collects messages, and $\phi_{2}$ can be thought of COMBINE function that updates the node feature with collected messages.
The authors simply extend the collected message $h_{e}$ of \eqref{eq:mp_twostep} to the set of collected messages $\{ h_{e} \}_{e \in E_{i}}$ for its application to hypergraphs:
\begin{equation}\label{eq:mp_hyper}
\text{(UniGNN)} \begin{cases} h_{e} = \phi_{1} (\{ x_{j} \} _{j \in e}), \\ x_{i} = \phi_{2} (x_{i}, \{ h_{e} \}_{e \in E_{i}}). \end{cases}
\end{equation}
It can be seen that if $E_{i} = \{ e = \{j\} | \forall j \in \mathcal{N}_{i} \}$, then the proposed UniGNNs \eqref{eq:mp_hyper} is easily reduced to GNNs \eqref{eq:mp_twostep} or \eqref{eq:mp}.
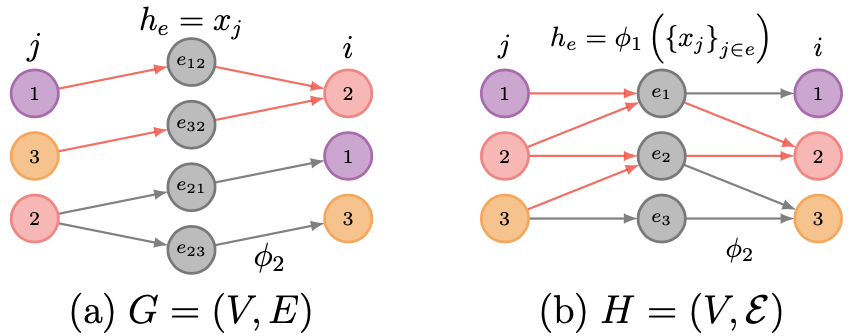Scheme of (a) GNNs \eqref{eq:mp_twostep} and the proposed (b) UniGNNs \eqref{eq:mp_hyper}
An example of the UniGNN is the UniGCN, an extension of the GCN to hypergraph.
The GCN can be formulated as
\begin{equation}
\tilde{x}_{i} = \frac{1}{\sqrt{d_{i}}} \sum \nolimits _{j \in \tilde{\mathcal{N}}} \frac{1}{\sqrt{d_{j}}}W x_{j},
\end{equation}
where $d_{i}$ is the degree of the node $x_{i}$.
Now, the extended UniGCN can be formulated as:
\begin{equation}
\tilde{x}_{i} = \frac{1}{\sqrt{d_{i}}} \sum \nolimits _{e \in \tilde{E}_{i}} \frac{1}{\sqrt{d_{e}}}W h_{e},
\end{equation}
where $d_{e} = \frac{1}{|e|} \sum_{i\in e} d_{i}$.
Other extensions of GNNs, including GAT, GIN, and GraphSAGE are referred to the original paper.
(They all substitute $\mathcal{N}$ to $E$ and $x_{j}$ to $h_{e}$)
The authors further address two issues (i) over-smoothing problem and the (ii) discriminative power of HyperGNNs. First, the over-smoothing problem is addressed by extending the GCNII, which is a GNN having strength in mitigating the over-smoothing problem, into UniGCNII. Second, the discriminative power is shown by a way similar to the GIN paper, which proves that the GNNs can be as powerful as the WL-test under injectivity of certain functions.
Demonstrate performance of UniGNN for hypernode classification tasks
The performance of UniGNNs are experimented with hypernode classification tasks.
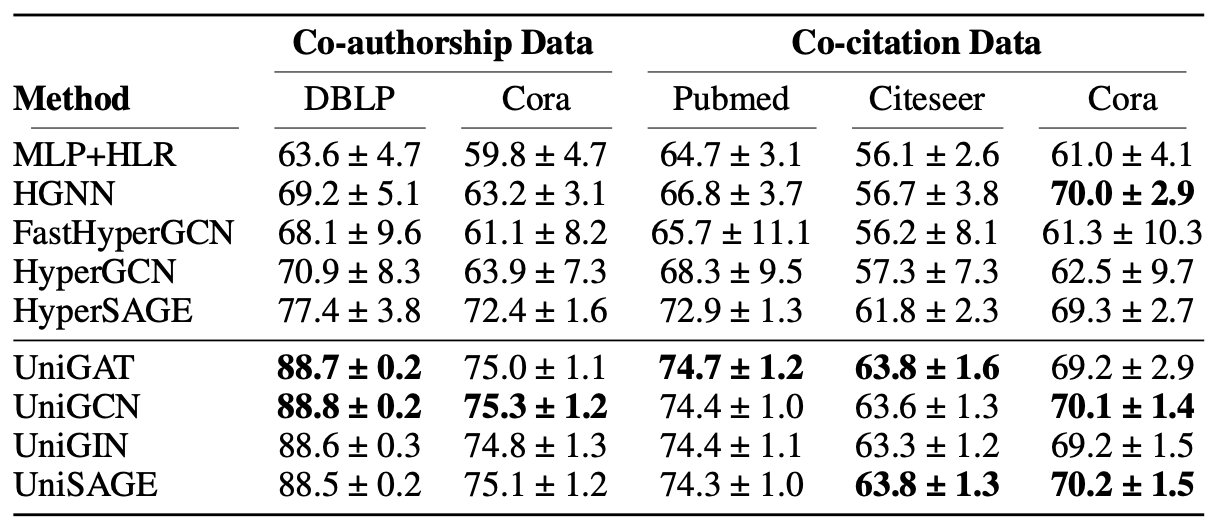Hypernode classification accuracy on co-authorship and co-citation datasets
It can be seen that the UniGNN models outperform other baseline HyperGNN models on hypernode classification tasks.
The UniGNN models also show exceptional performance on inductive learning tasks.
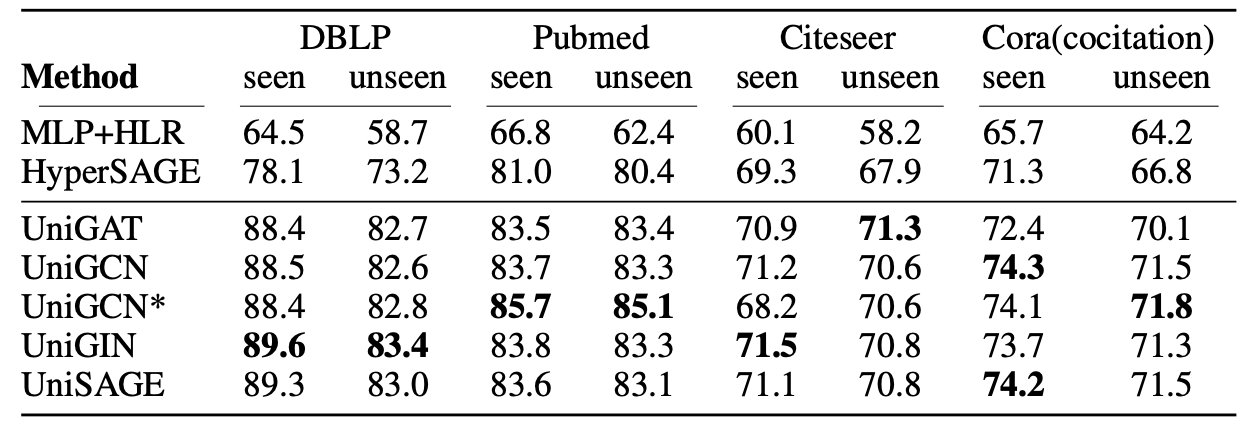Classification accuracy on inductive hypernode classification tasks
Since deeper GNN is related to an exaggerated over-smoothing problem, the UniGNN models are tested with varying network depths.
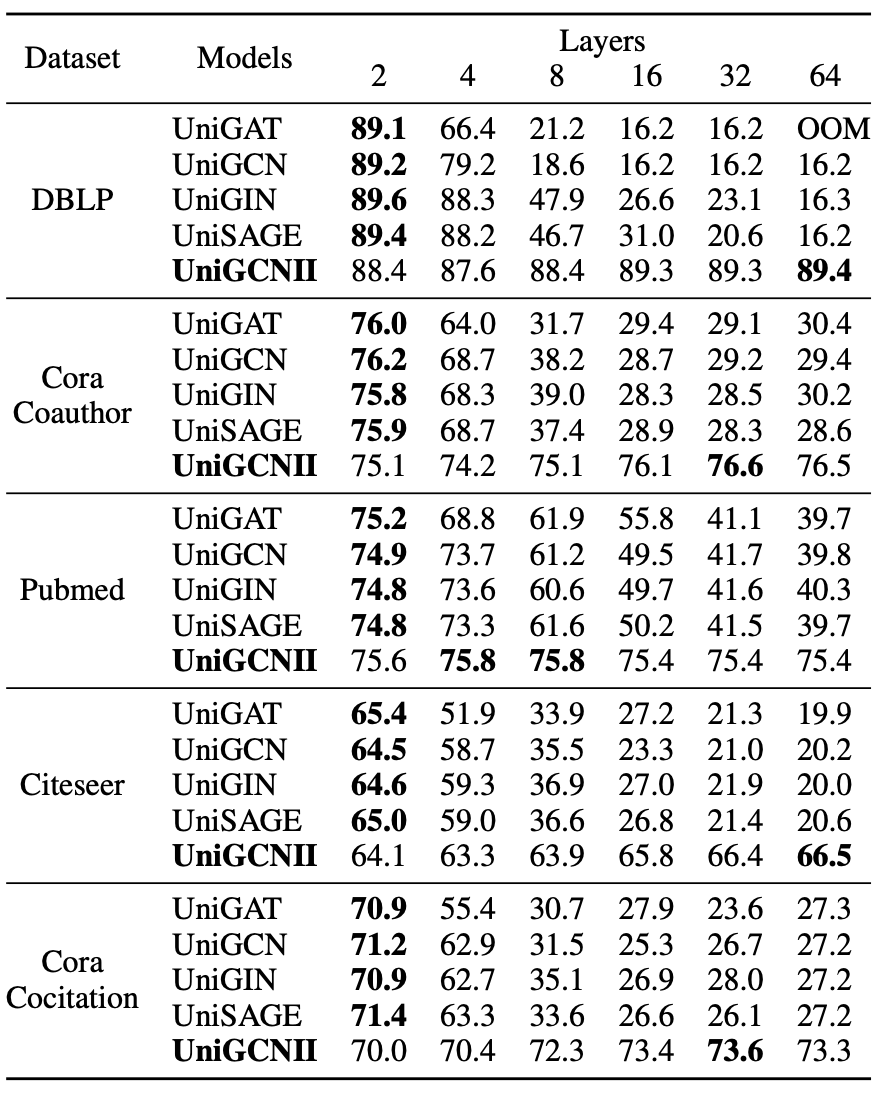Comparison of various UniGNN models w.r.t network depth
The Comparison of UniGNN models indicate that UniGAT, UniGCN, UniGIN, and UniSAGE show good classification accuracy when the network is shallow, while UniGCNII show good classification accuracy even when the network is deeper.
Other experimental results, including the effect of self-loop on UniGAT and UniGCN, are referred to the original paper.