Significance
Keypoints
- Propose a counterfactual learning framework to improve link prediction of GNNs
- Demonstrate performance of the proposed method with benchmark datasets
Review
Background
Link prediction is one of the key application tasks of the Graph Neural Networks (GNNs). Although the current scheme of predicting existence of link between two nodes by the association (e.g. dot product) of the two node features has shown impressive results, the authors address that the causal relationship between the graph structure and the existence of link can possibly improve the link prediction performance of the GNNs. Counterfactual learning for link prediction can be thought of learning to predict the existence of a certain link by asking “would the link exist or not if the graph structure became different?”.
Keypoints
Propose a counterfactual learning framework to improve link prediction of GNNs
A counterfactual question consists of a context, treatment, and outcome. Given a context (data), a counterfactual question asks what the outcome (existence of link) would have been if the treatment (cluster) had been different. Defining the context and outcome are straightforward, while the defining the treatment requires setting up how to cluster each nodes within the graph. The authors define the treatment as the community structure of the graph where the graph clustering method $c: \mathcal{V} \rightarrow \mathbb{N}$ maps a vertex to a cluster to define the treatment matrix $\mathbf{T}$: \begin{align} T_{i,j} = \begin{cases} 1,\quad &\text{if}c(v_{i})=c(v_{j}) \\ 0,\quad &\text{otherwise}. \end{cases} \end{align} The clustering method $c$ can be one of the Louvain, K-core, Spectral clustering, or any other. Now, the counterfactual link can be defined for any node pair $(v_{i},v_{j})$ as the link existence between other nodes with the opposite treatment (cluster). The authors specifically focus on the node pairs with opposite treatment and the nearest distance to the node pair of interest. Distance between the node pairs is calculated with the MVGRL.
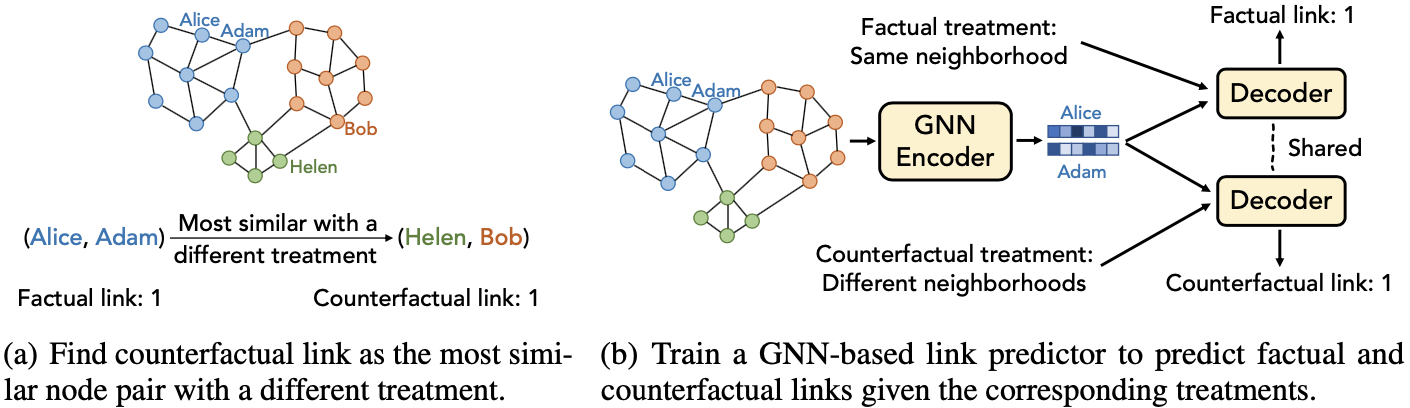Schematic illustration of the proposed method
Based on the counterfactual links, the link prediction is made by an encoder-decoder structure where the encoder is the GCN encoding the input node into the node feature matrix $\mathbf{Z}$ and the decoder $g$ decodes adjacency matrix from $\mathbf{Z}$ as: \begin{align} \hat{\mathbf{A}} = g(\mathbf{Z}, \mathbf{T}), \text{where} \hat{A}_{i,j} = \texttt{MLP}([\mathbf{z}_{i} \odot \mathbf{z}_{j},T_{i,j}]), \\ \hat{\mathbf{A}}^{\text{CF}} = g(\mathbf{Z}, \mathbf{T}^{\text{CF}}), \text{where} \hat{A}^{\text{CF}}_{i,j} = \texttt{MLP}([\mathbf{z}_{i} \odot \mathbf{z}_{j},T^{\text{CF}}_{i,j}]), \end{align} where $[\cdot ,\cdot]$ is the concatenation operation, and $\mathbf{T}^{\text{CF}}$ is the counterfactual treatment matrix. The predicted adjacency matrix $\hat{\mathbf{A}}$ and the predicted counterfactual adjacency matrix $\hat{\mathbf{A}}^{\text{CF}}$ are optimized with the cross-entropy loss, along with the balancing loss,
Demonstrate performance of the proposed method with benchmark datasets
The performance of the proposed method is evaluated on benchmark datasets including CORA, CiteSeer, PubMed, Facebook, and DDI.
Three encoders including GCN, GraphSage (GSAGE), and Jumping Knowledge Network (JKNet) are implemented along with baseline models.
The metrics Hits@20 and AUC demonstrate that the proposed CFLP improves the link prediction performance of the graph encoders.
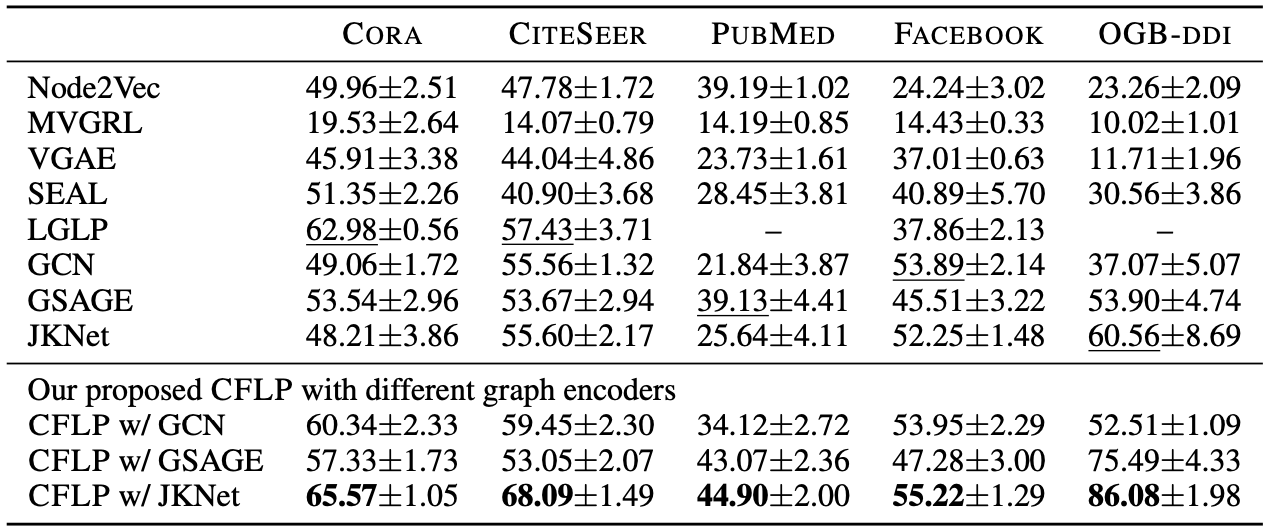Link prediction performance of the proposed method evaluated by Hits@20
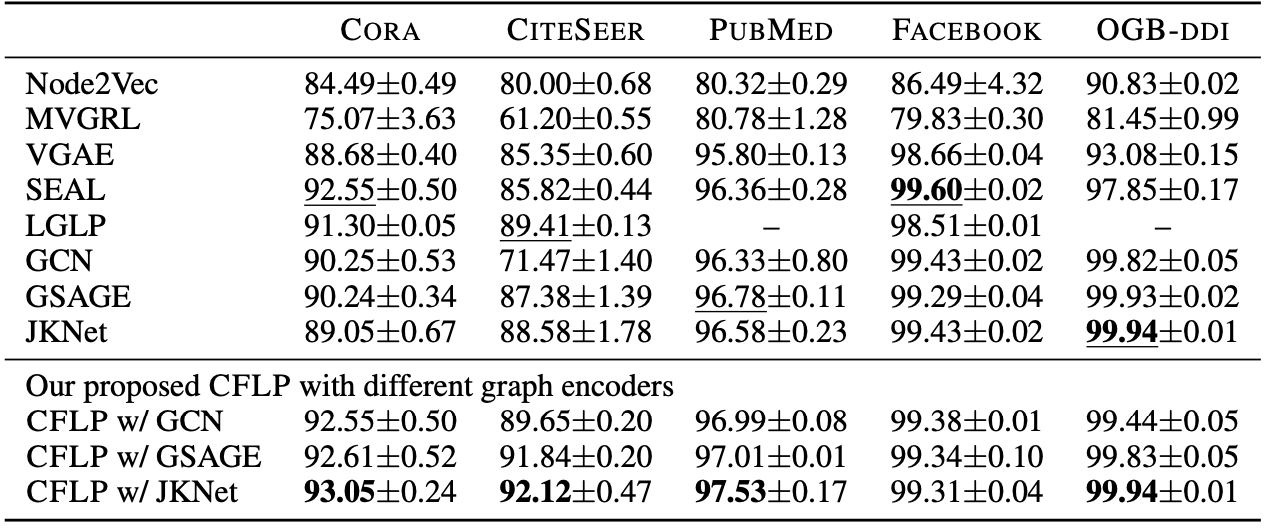Link prediction performance of the proposed method evaluated by AUC
Further studies on the treatment variables are referred to the original paper.