Significance
Keypoints
- Propose a Transformer based method for video action anticipation
- Demonstrate performance of the proposed method
Review
Background
Predicting future action from a video requires not only understanding the current frame, but also modeling temporal context across the frames. For example, a frame with a plate of food with a fork may suggest current action of eating, but anticipating this action before the frame is given requires reasoning over preceding events. The authors propose a transformer based method for predicting future action from video which learns to attend across space and time, and show state-of-the-art performance.
Keypoints
Propose a Transformer based method for video action anticipation
The authors propose anticipatory video transformer (AVT), which consists of two-step spatio-temporal attention with Transformers.
First step is the backbone, where each image frames of the video $\mathbf{X}_{t}$ is encoded into the latent $\mathbf{z}_{t}$ with a Vision Transformer.
Second step is the head, where the sequence of encoded latent is processed with a masked Causal Transformer Decoder as in the GPT-2 to output $\hat{\mathbf{z}_{t}}$.
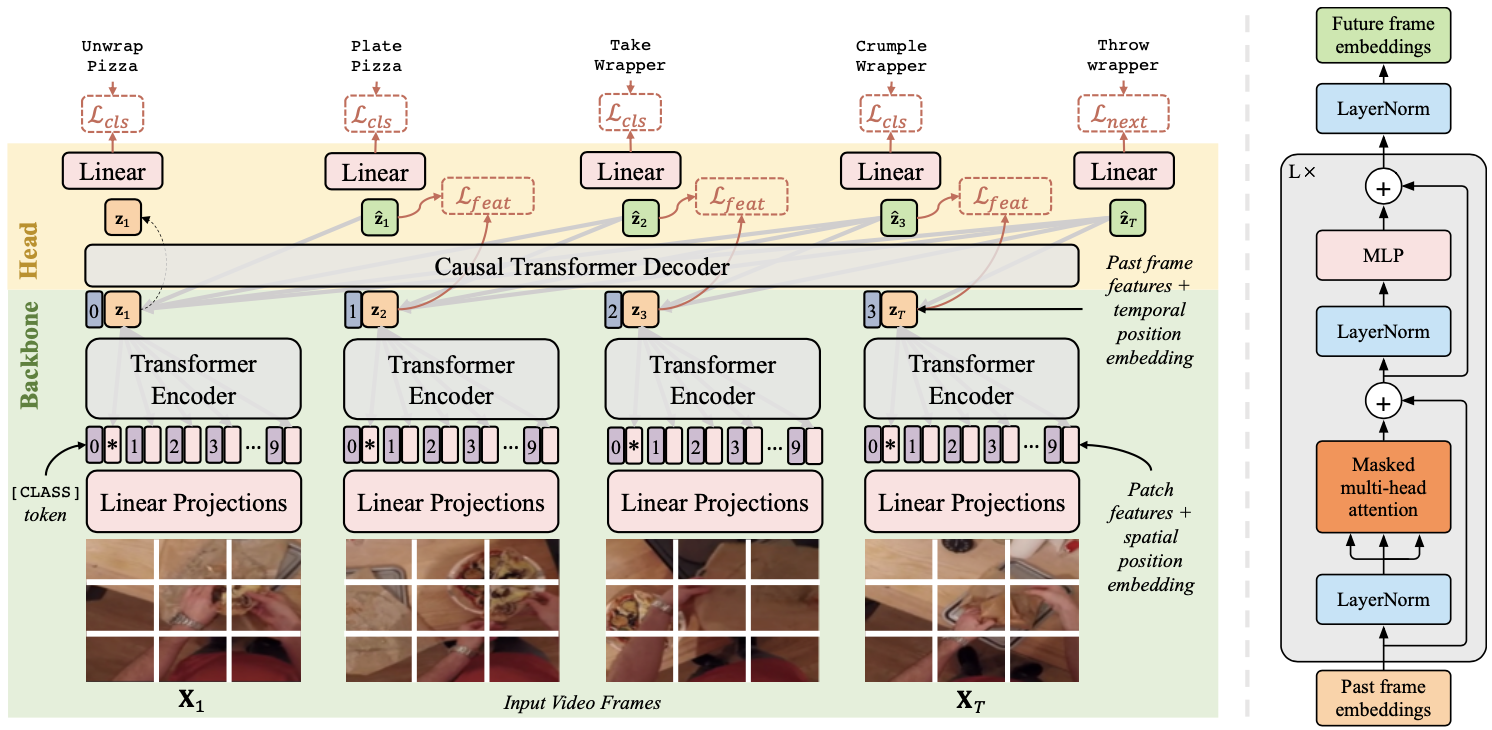Schematic illustration of the proposed method
The AVT is trained with a supervised cross-entropy loss with the labelled future action $c_{T+1}$: \begin{align} \mathcal{L}_{\text{next}} = -\log \hat{\mathbf{y}}[c_{T+1}], \end{align} where $T$ is the length of the given video sequence. For promoting the model to learn anticipatory features, the future feature matching loss: \begin{align} \mathcal{L}_{\text{feat}} = \sum^{T-1}_{t=1} || \hat{\mathbf{z}}_{t}-\mathbf{z}_{t+1} ||^{2}_{2}, \end{align} and the action class level anticipative loss: \begin{align} \mathcal{L}_{\text{cls}} = \sum^{T-1}_{t=1} \mathcal{L}^{t}_{\text{cls}}; \mathcal{L}^{t}_{\text{cls}}=\begin{cases} -\log \hat{\mathbf{y}}_{t}[c_{t+1}], \quad &\text{if} c_{t+1}\geq 0 \\ 0, &\text{otherwise}\end{cases}. \end{align} The final loss $\mathcal{L}$ is defined as the sum of the above three losses.
Demonstrate performance of the proposed method
The proposed model is experimented on four popular datasets, EpicKitchens-100 (EK100), EpicKitchens-55 (EK55), EGTEA Gaze+, and 50-Salads (50S).
The proposed method outperformed previous methods and other submissions from the CVPR 2021 EK100 challenge.
Performance of the proposed method on the EK100 dataset
The AVT also outperformed all other previous methods on the validation and the seen (S1) and unseen (S2) test data of the EK55 dataset.
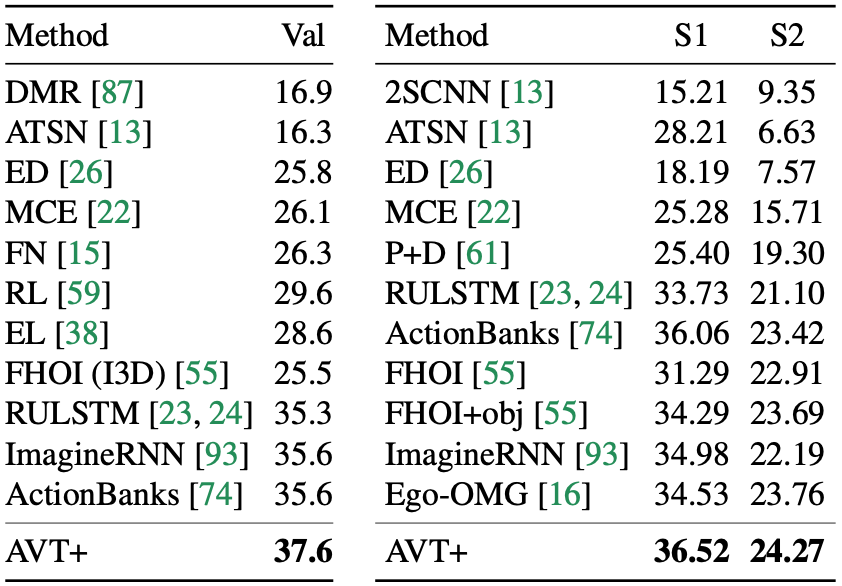Performance of the proposed method on the EK55 dataset
This exceptional performance of AVT was apparent in the EGTEA Gaze+ dataset and the 50-Salads dataset too.
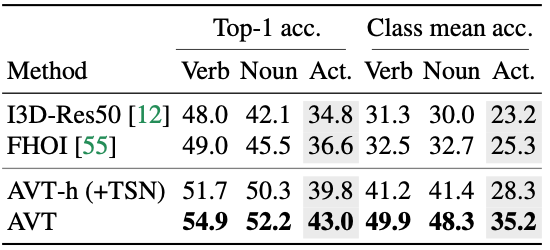Performance of the proposed method on the EGTEA Gaze+ dataset
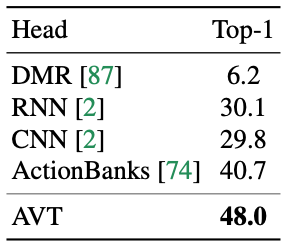Performance of the proposed method on the 50-Salads dataset
Anticipation can be computed for a longer-term with the AVT by an autoregressive approach.
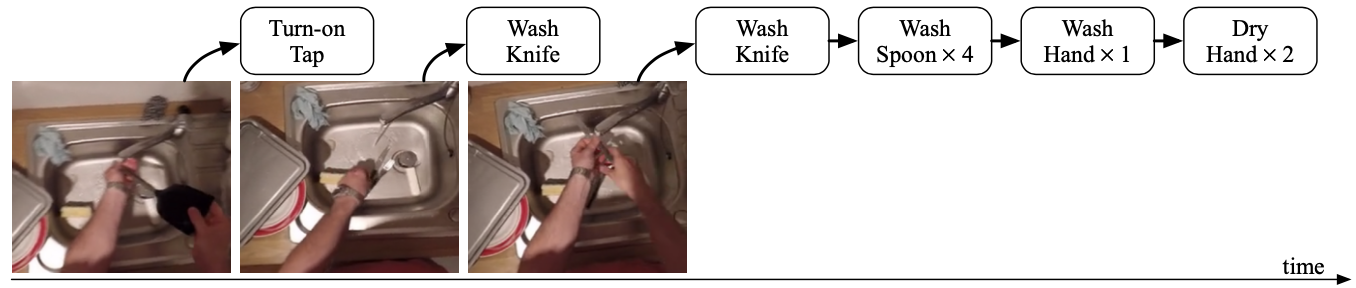Long-term anticipation by rolling out predictions autoregressively
Other results including ablative study and the qualitative analysis of the attention are referred to the original paper.