[2104.03310] Regularizing Generative Adversarial Networks under Limited Data

• Propose a discriminator regularization function for training GAN under limited data
• Theoretically show relationship between the regularized loss and LeCam-divergence
• Experimentally show improvement in GAN training dynamics

Background

Generative adversarial network (GAN) is a class of the generative models, which employs an adversarial training between the generator $G$ and the discriminator $D$ to minimize the divergence between the true data distribution $p_{data}$ and the generated data distribution with random noise $z$ as prior $p_{G(z)}$. Although GANs are capable of generating realistic images, training of the GANs requires a large amount data and the learning dynamic is not very stable. To overcome the instability of the training dynamics, it has been proposed to minimize different loss function (LSGAN, WGAN) or to regularize the weight matrices (Spectral normalization). However, not many works have addressed the issue of training the GANs with limited dataset. This work presents a simple way to improve the quality of the generated image with GANs by adding a regularization to the discriminator loss during training.

Keypoints

Propose a discriminator regularization function for training GAN under limited data

Training the GAN alternates between maximizing the discriminator loss $V_{D}$ and minimizing the generator loss $L_{G}$. \begin{align} \underset{D}{\max}V_{D}, \quad V_{D} &= \underset{\mathbf{x}\sim\mathcal{T}}{\mathbb{E}} [ f_{D}(D(\mathbf{x})) ] + \underset{\mathbf{z}\sim\mathcal{N}(0,1)}{\mathbb{E}} [ f_{G}(D(G(\mathbf{z}))) ] \\ \underset{G}{\max}L_{G}, \quad L_{G} &= \underset{\mathbf{z}\sim\mathcal{N}(0,1)}{\mathbb{E}} [ g_{G}(D(G(\mathbf{z}))) ], \end{align} where $\mathcal{T}$ is the training dataset distribution, and $f$, $g$ are loss functions for training the GAN.

To improve the performance when only a limited amount of data can be sampled from the training data distribution $\mathcal{T}$, the authors propose to add a regularization term $R_{LC}$ to the $V_{D}$, arriving at the final discriminator loss $L_{D}$: \begin{equation}\label{eq:proposed} L_{D} = -V_{D} + \lambda R_{LC}, \end{equation} where $\lambda$ is the coefficient hyperparameter and the $R_{LC}$ is defined as \begin{equation} R_{LC} = \underset{\mathbf{x}\sim\mathcal{T}}{\mathbb{E}} [ || D(\mathbf(x)) - \alpha_{F}||^{2} ] + \underset{\mathbf{z}\sim\mathcal{N}(0,1)}{\mathbb{E}} [ || D(G(\mathbf(z))) - \alpha_{R}||^{2} ]. \end{equation} The $\alpha_{R}$ and the $\alpha_{F}$ are exponential moving average $\alpha^{(t)} = \gamma \times \alpha^{(t-1)} + (1-\gamma) \times v^{(t)}$ of the discriminator prediction for real and fake image inputs. Note that the distance between the real image input and the fake moving average is minimized, and vice versa.

Theoretically show relationship between the regularized loss and LeCam-divergence

The authors provide two propositions to claim that:

1. Minimizing WGAN objective with the proposed regularization follows minimizing the LeCam(LC)-divergence
2. LC-divergence is an $f$-divergence with properties suited for GAN training.

Derivation of the two propositions is not very complicated so is referred to the original paper. After the relationship between the regularized WGAN objective and the LC-divergence is shown, it is insisted that minimizing the LC-divergence is more stable when the number of training data is limited because it is more robust to extreme values. 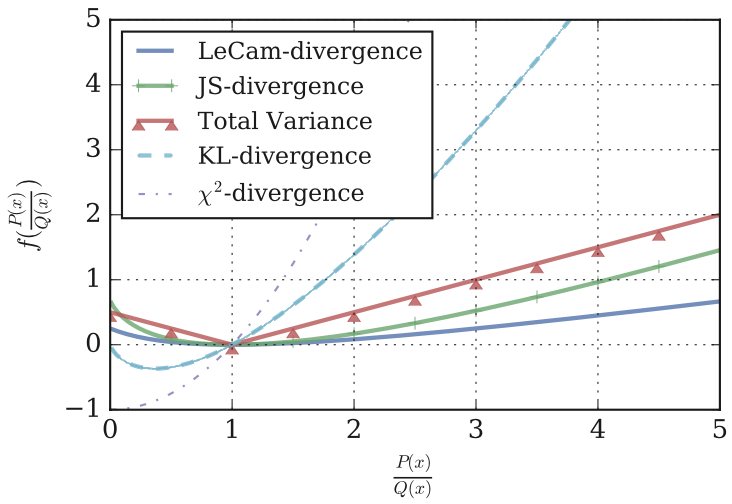LC-divergence is more robust to extreme values than other $f$-divergences

In my opinion, it is not very straightforward to think that the stability of the function leads to the stability of the training when the number of data is limited. Furthermore, if we assume that it is true, then the above figure indicates that training with the vanilla GAN (JS-divergence) is more stable than training with the LSGAN ($\chi^{2}$-divergence) or the EBGAN (Total Variance).

Experimentally show improvement in GAN training dynamics

Improvement in GAN training dynamics is demonstrated by experiments using the CIFAR-10/CIFAR-100/ImageNet datasets and BigGAN(conditional)/StyleGAN2(unconditional) models with Inception score (IS)/Fréchet inception distance (FID) as the metric. The authors prove the utility of the proposed regularization \eqref{eq:proposed} by extensive quantitative and qualitative experiments, and can be summarized as:

1. Image generation quality is relatively well preserved when the training dataset is limited
2. Can further complement data augmentation strategies for GAN
3. Training dynamic of GAN is stabilized

Qualitative and quantitative performance with limited dataset, along with synergistic effect with data augmentation (DA) 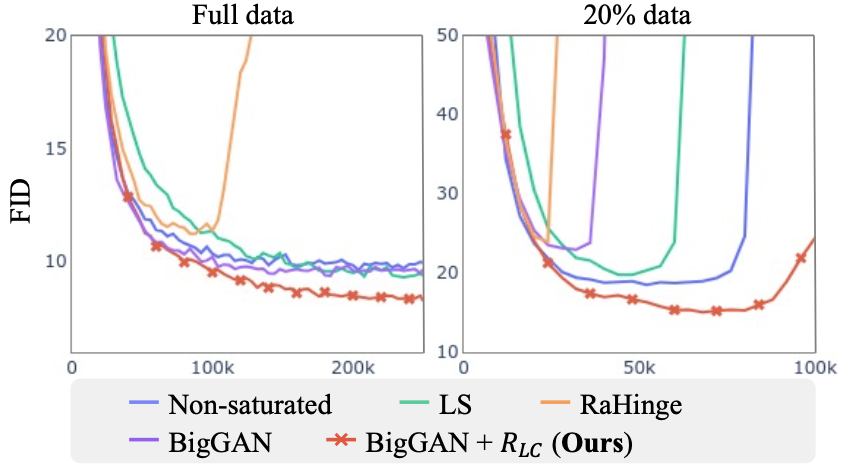Training dynamic is stabilized, especially when the training dataset is limited

• A Picture is Worth a Thousand Words: Principled Recaptioning Improves Image Generation
• Tackling the Generative Learning Trilemma with Denoising Diffusion GANs
• Image Synthesis and Editing with Stochastic Differential Equations
• RewriteNet: Realistic Scene Text Image Generation via Editing Text in Real-world Image
• ViTGAN: Training GANs with Vision Transformers