Significance
Keypoints
- Propose an MLP only architecture for image classification
- Demonstrate comparable classification performance of the proposed ResMLP to CNNs and ViTs
- Analyze the trained weights of the ResMLP model
Review
Background
Multi-layer perceptrons (MLP) were first suggested as a basic architecture of the deep neural networks long time ago. However, it has been thought that neural networks composed of only MLPs are not capable of, or efficient, for learning representation of image data. Convolution neural networks (CNNs) have been a de facto choice of architecture for image classifications, and Transformer based methods (ViTs) are starting to take over CNNs. Strikingly, a recent work called MLP-Mixer have shown that replacing the self-attention part of the ViT to an MLP can still work well for image classification. This study is similar to the idea, and also confirms this recent possibility of MLP based models. Furthermore, the proposed architecture ResMLP does not require any form of normalization of minibatch/channel information, and is capable of distilling knowledge from a pre-trained CNN.
Keypoints
Propose an MLP only architecture for image classification
The proposed ResMLP architecture is extremely simple, including only a set of matrix multiplications, skip-connections, GeLU nonlinearity, and affine transformations.
The proposed ResMLP architecture
An input image is first split and stacked into non-overlapping patches of $\mathbf{X}\in \mathbb{R}^{N^{2}\times d}$ where $N$ is the patch size and $d$ is the length of the feature vector.
Given an affine transformation with learnable scale and shift parameters $\alpha$ and $\beta$:
\begin{equation}
\texttt{Aff}_{\alpha,\beta}(\mathbf{x}) = \texttt{Diag}(\alpha)\mathbf{x} + \beta,
\end{equation}
a ResMLP layer is defined as following:
\begin{align}
\mathbf{Z} &= \mathbf{X} + \texttt{Aff} ((\mathbf{A} \texttt{Aff} (\mathbf{X})^{\top})^{\top}),\label{eq:mlp} \\ \mathbf{Y} &= \mathbf{Z} + \texttt{Aff} (\mathbf{C} \texttt{GELU} (\mathbf{B} \texttt{Aff} (\mathbf{Z}))). \label{eq:ff}
\end{align}
The matrices $\mathbf{A}$, $\mathbf{B}$ and $\mathbf{C}$ are learnable MLP parameters.
The \eqref{eq:mlp} corresponds to replacing the self-attention layer in the ViTs, while \eqref{eq:ff} corresponds to the feed-forward layer in the ViTs.
It should be noted that no LayerNorm is applied in the ResMLP, further obtaining efficiency during inference.
Also, not any form of positional embedding or extra token is required in the proposed architecture.
Demonstrate comparable classification performance of the proposed ResMLP to CNNs and ViTs
Main experiments are conducted on ImageNet-1k dataset with 1.2M images over 1,000 object categories.
The ResMLP is trained in a supervised setting with a softmax classifier and cross-entropy loss to demonstrate its performance on image classification.
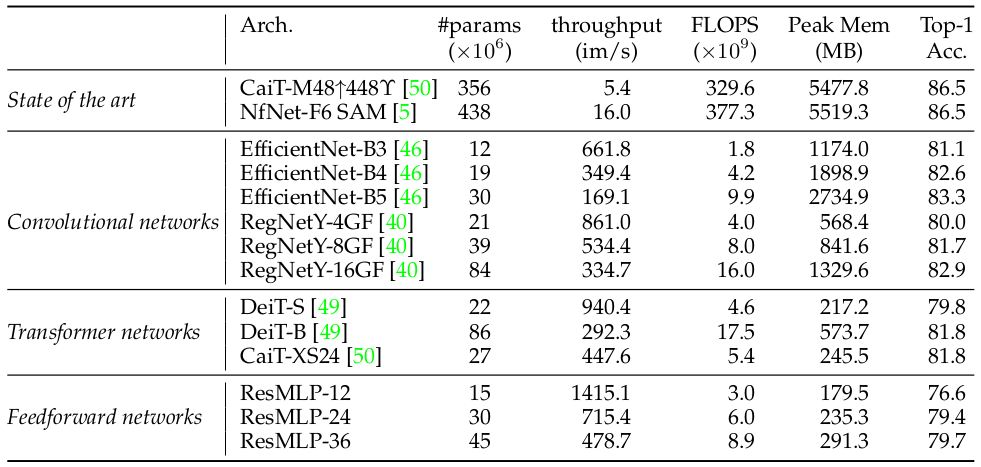Classification performance of ResMLP compared with CNNs and ViTs
It cannot be said that the ResMLP outperforms CNN- or ViT-based models on classification accuracy.
However, its comparable performance to the Convolutional and Transformer networks is very encouraging for a newborn baseline MLP model, which has a lot of room for further improvement.
The ResMLP has not been compared with the MLP-Mixer, which was published about a week ago, and has similar architecture with LayerNorm instead of affine transformation.
Knowledge distillation from a pre-trained CNN (RegNety-16GF) could further improve the performance of the ResMLP.
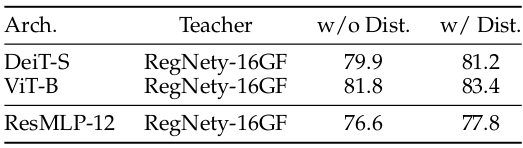Knowledge distillation results
Ablation studies are also performed for normalization layers, pooling layers, and patch communication (replacing MLP with 3$\times$3 convolution).
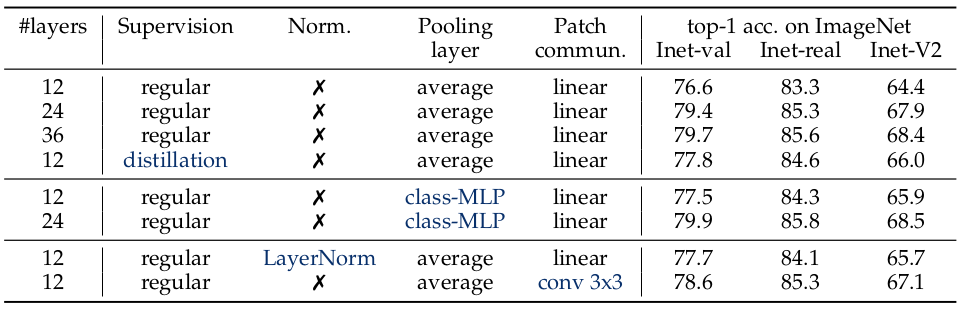Ablation study results
Analyze the trained weights of the ResMLP model
Since the ResMLP model has a single learnable matrix $\mathbf{A}$ which replaces the self-attention layer, visualization and analysis of the learned parameter is straightforward.
Exemplar visualizations of matrix $\mathbf{A}$ of \eqref{eq:mlp} for layers 1, 4, 7, 10, 20, and 22
Interestingly, it can be seen that the earlier layers resemble convolution operations with shifting weights as in Toeplitz matrices.
Another property of the matrix $\mathbf{A}$ is sparsity.
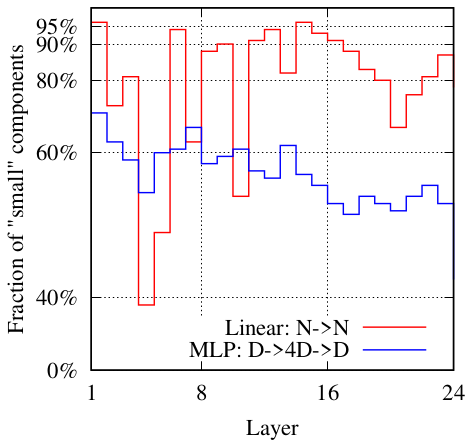Sparsity of the learnable matrices
The plot above indicates that all learnable matrices $\mathbf{A}$, $\mathbf{B}$, and $\mathbf{C}$ are sparse, and $\mathbf{A}$ (red line) is especially more sparse having greater number of small components than $\mathbf{B}$ and $\mathbf{C}$ (blue line).
Further preliminary experiment results are referred to the original paper. Encouraging works on MLP-only architectures for image data are being introduced recently. Can it be the beginning of Matrix multiplication is all you need?